Растяжение и сжатие

Растяжение (сжатие) – это вид деформации, при котором в поперечном сечении стержня возникает только продольная растягивающая (сжимающая) сила.

В условиях растяжения находится стержень под действием осевых сил на краях (рис. 9.11)

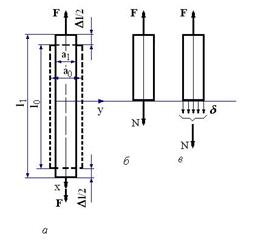
Рис. 9.11

Передача такого усилия к стержню может осуществляться различными способами, например, через гайку и головку болта в резьбовом соединении. Но во всех случаях равнодействующая внешних сил будет равна F.

Модель растягиваемого стержня используется в расчетах болтов, ремней передач, стержней ферм, лопаток турбин и т. д.

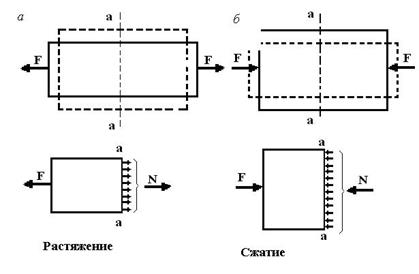
Рис. 9.121

При осевом растяжении и сжатии внутренние силы в поперечном сечении могут быть заменены одной силой, направленной вдоль оси стержня (рис.9.12) — продольной силой N. В случае когда сила направлена к отброшенной части наружу, имеет место растяжение (рис.9.12, a). Наоборот, если она направлена от отброшенной части внутрь (рис. 9.12, б), имеет место сжатие. Будем считать силу N положительной, если она растягивает стержень, и отрицательной – если сжимает.

Рассмотрим пример (рис.9.13, а).

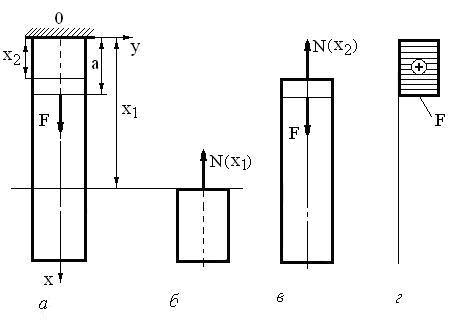
Рис. 9.13

Здесь сила F приложена в сечении x = a. В любом сечении при x ₁ ≥ a (рис.9.13, б) N (x ₁) = 0. Это означает, что часть стержня на этом участке под силой F не нагружена. Проведем второе сечение x ₂ ≤ a (рис.9.13, в) и рассмотрим равновесие нижней части. Уравнение равновесия относительно оси x:

,

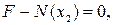
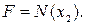График изменения внутренних сил (эпюра) приведен на рис. 9.13, г. Каждая ордината эпюры равна значению N в данном сечении. Эпюру строят на линии, проведенной параллельно оси стержня.

Нормальное напряжение в поперечном сечении стержня при растяжении равно поделенной на площадь сечения продольной силе в этом сечении:

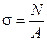(9.1)

Таким образом, часть стержня, находящаяся под силой F, не напряжена.

При сжатии стержня напряжения имеют лишь другой (отрицательный) знак (нормальная сила направлена в тело стержня).

Под действием осевых растягивающих сил стержень постоянного сечения площадью 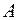удлиняется на величину

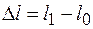, (9.2)

где l ₁, l ₀ − длины стержня в деформированном и недеформированном состоянии, ∆ l − абсолютное (полное) удлинение при растяжении (в случае сжатия данная величина называется абсолютным (полным) укорочением).

Экспериментально установлено, что чем больше l ₀, тем больше ∆ l. Наиболее удобной мерой деформации является относительное удлинение - удлинение, отнесенное к первоначальной длине стержня:

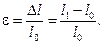(9.3)

Величина ε обычно выражается в процентах от начальной длины. При сжатии ε называют относительным укорочением.

Из опыта следует, что удлинение стержня в осевом направлении сопровождается уменьшением его поперечных размеров. Следовательно, при растяжении и сжатии возникает не только продольная, но и поперечная деформация стержня.

Если первоначальная ширина стержня a ₀, то под действием сил F она уменьшится на величину

Δ а = a ₁ ‑ a ₀. (4)

Относительная поперечная деформация будет определяться выражением

(5)

Знак «минус» показывает, что при растяжении стержня поперечные размеры уменьшаются.

Отношение поперечной деформации к продольной при растяжении (сжатии), взятое по абсолютной величине, называют коэффициентом Пуассона:

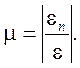(9.6)

На основании экспериментов получено: для сталей μ = 0, 25...0, 3; для алюминиевых сплавов μ = 0, 3...0, 35; для медных сплавов μ = 0, 35.

Между напряжениями и малыми деформациями существует линейная зависимость, называемая законом Гука. Для центрального растяжения (сжатия) она имеет вид

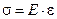, (9.7)

где E — коэффициент пропорциональности, именуемый модулем упругости (модулем Юнга). По физическому смыслу модуль упругости — напряжение, которое вызывает деформацию ε = 1 (удлинение стержня, равное первоначальной длине). По данным экспериментов: E = (2...2, 2)∙ 10⁵ МПа — для сталей; E = 1, 1∙ 10⁵ МПа — для титановых сплавов; E = 0, 7∙ 10⁵ МПа — для алюминиевых сплавов.

Для некоторых материалов (например, коррозионно-стойких сталей) закон Гука является приближенным даже при сравнительно небольших деформациях.

С учетом выражений (9.1) и (9.3) закон Гука для растянутого (сжатого) стержня (9.7) можно записать в виде

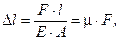(9.8)

где μ — коэффициент продольной податливости стержня, показывающий удлинение (укорочение) стержня, вызываемое растягивающей (сжимающей) силой F = 1 Н. Произведение E·A называют жесткостью сечения стержня при растяжении (сжатии).

Для стержня переменного (ступенчатого) сечения удлинения определяют по участкам (ступеням) и результаты суммируют алгебраически:

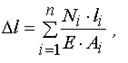(9.9)

где i − номер участка (i =1, 2,..., n).

При расчете упругих перемещений стержня от нескольких сил часто применяют принцип независимости действия сил: перемещение стержня от действия группы сил может быть получено как сумма перемещений от действия каждой силы в отдельности.

Экспериментально установлено, что модуль упругости E при умеренном нагреве незначительно меняется с температурой, а коэффициент α практически не зависит от напряжения σ. Для стали эта зависимость имеет место до температуры 300...400°С. При более высоких температурах необходимо учитывать зависимость модуля упругости E от температуры t.

Следует отметить, что формулы (9.7)...(9.8) выведены в предположении, что стержень растянут силами, равномерно распределенными по сечению (рис. 9.14, а).

При растяжении сосредоточенными силами, как показывают эксперименты и расчеты методами теории упругости, сечения стержня вблизи мест приложения внешних сил в результате деформации искривляются (рис. 9.14, б) возникают большие местные деформации и напряжения.

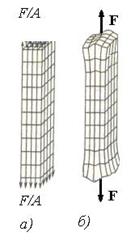
Рис. 9.14

Решение задач на тему «Растяжение и сжатие»

Задача 1

Построить эпюру распределения продольных сил и нормальных напряжений по длине бруса (рис. 9.15). Определить перемещение сечения А − А.

Е = 2·10⁵ МПа, А = 2 см².

.

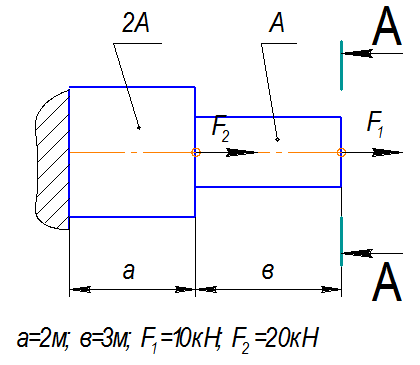
Рис. 9.15

Решение

Разобьем брус на отдельные участки, начиная со свободного конца. Границы участков – сечения, в которых приложены внешние силы и места изменения размеров поперечного сечения. Имеем два участка.

Применяя метод сечений, отбрасываем левую часть бруса. Проведем произвольное сечение на первом участке и рассмотрим равновесие оставшейся части, изображенной на рис. 9.16, проектируя на ось z продольные силы F ₁, N ₁.

F ₁ - N ₁ =0

N ₁ = F ₁=10 кН

Проведем произвольное сечение на втором участке и рассмотрим равновесие оставшейся части изображенной на рис. 9.16, проектируя на ось z продольные силы F ₁, F ₂, N ₂:

F ₁ + F ₂- N ₂ = 0;

N ₂ = F ₁ + F ₂=10+20 = 30 кН.

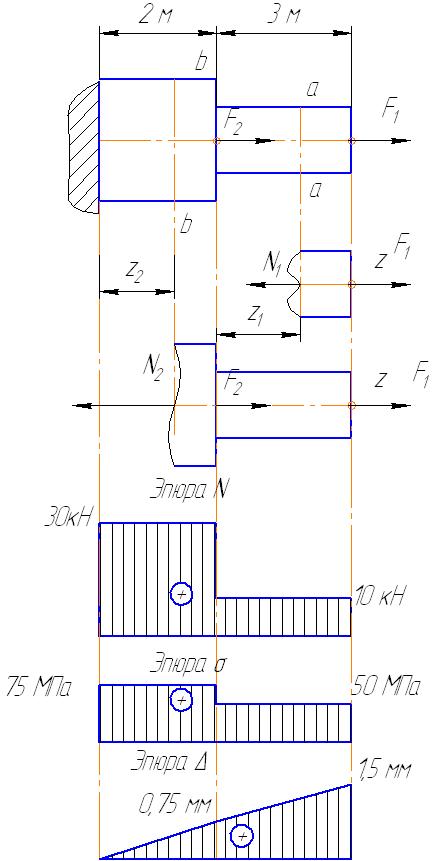
Рис. 9.16

Построим график (эпюру), показывающую, как изменяется N по длине бруса. В пределах одного участка продольная сила не меняется, поэтому эпюра N ограничена линией параллельной оси.

Эпюру нормальных напряжений получим, разделив значения N на соответствующие площади поперечных сечений.

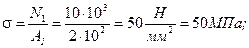
Эпюрой перемещений называется график, показывающий закон изменения величин перемещений поперечных сечений бруса по его длине. Эпюру перемещений строят, начиная с защемленного конца. Перемещение произвольного сечения b − b бруса на участке 2 равно удлинению части бруса длиной z ₂. На конце второго участка z ₂ = 2 м.

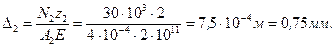
Перемещение произвольного сечения a − a бруса на участке 1 равно удлинению части бруса длиной z ₁. На конце первого участка z ₁ = 3 м:

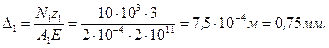
Перемещение сечения А − А равно сумме перемещений на первом и втором участке:

Δ _АА = Δ ₁ + Δ ₂ =0, 75+0, 75=1, 5 мм.