Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Изучение связи между качественными признаками на основе таблиц сопряженности

Построение таблиц, в которых дается комбинационное распре­деление единиц совокупности по двум признакам, применимо не только к количественным, но и к неколичественным, т.е. качест­венным, или атрибутивным, признакам (пол, образование, семей­ное положение, профессия, форма собственности, вид заболева­ний, вид преступлений и т.п.).

Качественные признаки, взаимосвязи между ними, их влияние на другие показатели (в том числе и количественные) особенно часто приходится изучать при проведении различных социологи­ческих исследований путем опроса или анкетирования.

В таких случаях о зависимости ответов на те или иные вопросы от других признаков единиц наблюдения судят, исходя из комби­национного распределения единиц совокупности по двум атрибу­тивным признакам (или одному атрибутивному, а другому — коли­чественному), т.е. анализируя таблицы взаимной сопряженности. Последние могут иметь разную размерность.

Простейшая форма таблицы взаимной сопряженности — таб­лица «четырех полей». В ней по каждому при­знаку выделяется только две группы, чаще всего по альтернативно­му принципу («да» — «нет», «хорошо» — «плохо» и т.д.). Пример такой таблицы приведен ниже. В ней указаны условные данные о распределении 500 опрошенных человек по двум показа­телям: наличие (отсутствие) у них прививки против гриппа и факт заболевания (не заболевания) гриппом во время его эпидемии.

Таблица

Таблица «четырех полей»

Применительно к таблице «четырех полей», частоты которых можно обозначить через а, Ь, с, d, коэффициент ассоциации выра­жается формулой

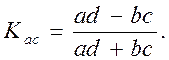
Для распределения, при­веденного выше, имеем:

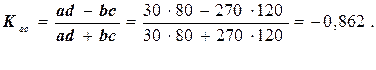
Задача

Для четырех пар значений (x _i y _i), приведенных в табл., определите линейные коэффициенты корреляции Пирсона: r ₁, r ₂, r ₃, r ₄.

Ответ. r ₁ = 0, 947; r ₂ = - 0, 937; r ₃ = -0, 591; r ₄ = 0, 01.

Задачи

Задача 1. В урне 30 шаров: 20 белых и 10 черных. Вы­нули подряд четыре шара, причем каждый вынутый шар возвращается в урну перед извлечением следующего и шары в урне перемешиваются. Какова вероятность того, что среди вынутых 4 шаров будет 2 белых?

Решение. Вероятность извлечения белого шара p = 20/30 = 2/3

можно считать одной и той же во всех четы­рех испытаниях; q = 1 - p = 1/3. Применив предыдущую формулу, получаем

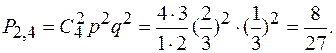
Задача 2. Вероятность появления события А равна 0, 4.
Какова вероятность того, что при 10 испытаниях собы­тие А появится не больше трех раз?

Решение. Здесь p = 0, 4, q = 0, 6.

Найдем вероятности появления события А:

0 раз - Р _{0, 10} = q ¹⁰;

1 раз - Р _{1, 10} = 10 рq ⁹;

2 раза - Р_{2, 10} = 45 р ² q ⁸;

З раза – Р _{3, 10} = 120 р ³ q ⁷.

Вероятность того, что событие А появится не больше
З раз, определится равенством Р = Р _{0, 10} + Р _{1, 10} + Р _{2, 10} + Р_{3 , 10}.

т. е.

Р = 0, 6 ⁷ • (0, 216 + 1, 44 + 4, 32 + 7, 68), Р ~ 0, 38.

Задача 3. Определить вероятность того, что в семье, имеющей пять детей, будет три девочки и два мальчика. Вероятности рождения мальчика и девочки будем счи­тать одинаковыми.

Решение. Вероятность рождения девочки р = 0, 5, тогда q =1 - р = 0, 5 (вероятность рождения мальчика). Решение находим по формуле

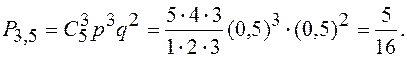
Условная вероятность события H_i в предположении, что событие А имеет место, определяется по так назы­ваемой формуле Бейеса:

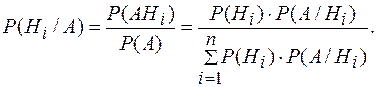
Вероятности Р(H _i/ А), вычисленные по формуле Бей­еса, часто называют вероятностями гипотез.

Задача 4. Имеется 4 урны. В первой урне 1 белый и 1 черный шары. Во второй урне 2 белых и 3 черных шара. В третьей урне 3 белых и 5 черных шаров, В четвертой урне 4 белых и 7 черных шаров. Событие H _i —выбор i-й урны (i = l, 2, 3, 4). Дано, что вероятность выбора i-й урны равна 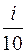, т. е. Р (H ₁) = 0, 1; Р (H ₂) = 0, 2; Р (H ₃) = 0, 3; Р (H ₄) = 0, 4.

Выбирается наугад одна из урн и вынимается из нее шар. Найти вероятность того, что этот шар белый.

Решение. Из условия следует, что Р (А/Н ₁) = 0, 5 (условная вероятность извлечения белого шара из пер­вой урны).

Р (А/Н ₂) = 2/5; Р (А/Н ₃) = 3/8; Р (А/Н ₄) = 4/11.

Вероятность извлечения белого шара, находим по фор­муле полной вероятности:

Р (А) = Р (Н ₁)• Р (А/Н ₁) + Р (H ₂)• Р(А/Н₂) + Р (H₃)• Р (А/Н ₃) + Р (H ₄)• Р (А/Н ₄) =

= 1707/4400.

Задача 5. Имеются три одинаковых по виду ящика. В пер­вом ящике 20 белых шаров. Во втором ящике 10 белых и 10 черных шаров. В третьем ящике 20 черных шаров. Из выбранного наугад ящика вынули белый шар.

Вычислить вероятность того, что шар вынут из первого
ящика.