Нормальный закон распределения характеризуется плотностью

Биномиальный закон распределения. Закон Пуассона

Если вероятность наступления случайного события в каждом испытании равна р, то, как известно, вероятность того, что при п испытаниях событие осуществится т раз, определяется формулой Бернулли:

Закон распределения случайной величины X, могущей принимать п +1 значение (0, 1,...., п), описываемый формулой Бернулли, называется биномиальным.

Закон распределения случайной величины X, могущей принимать любые целые неотрицательные значения (0, 1,...., п), описываемый формулой

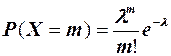
носит название закона Пуассона.

Математическое ожидание и дисперсия случайных ве­личин, распределенных по биномиальному закону и закону Пуассона, определяются по следующим формулам:

а) биномиальный закон: М (х) = пр; D(x) = npq;

б) закон Пуассона: М(х) = λ; D(x) = λ.

Нормальный закон распределения и функция Лапласа

Нормальный закон распределения характеризуется плотностью

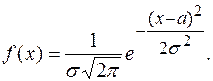
Задача 1. Определите математическое ожидание случай­ной величины с равномерным распределением.