Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Формальная постановка задачи классификации

Будем использовать следующую модель задачи классификации. Ω – множество объектов распознавания (пространство образов). ω: ω 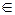Ω – объект распознавания (образ). g (ω): Ω → M, M = {1, 2,..., m } – индикаторная функция, разбивающая пространство образов Ω на m непересекающихся классов Ω 1, Ω 2,..., Ω m. Индикаторная функция неизвестна наблюдателю. X– пространство наблюдений, воспринимаемых наблюдателем (пространство признаков). x (ω): Ω → X – функция, ставящая в соответствие каждому объекту ω точку x (ω) в пространстве признаков. Вектор x (ω) - это образ объекта, воспринимаемый наблюдателем. В пространстве признаков определены непересекающиеся множества точек Ki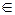 X, i = 1, 2..., m, соответствующих образам одного класса. :  – решающее правило – оценка для g (ω) на основании x (ω), т.е. . Пусть x _j = x( ω _j ), j = 1, 2..., N – доступная наблюдателю информация о функциях g (ω) и x (ω), но сами эти функции наблюдателю неизвестны. Тогда (g _j, x _j), j  1, 2..., N – есть множество прецедентов.

Задача заключается в построении такого решающего правила , чтобы распознавание проводилось с минимальным числом ошибок. Обычный случай – считать пространство признаков евклидовым, т.е. X= R^l . Качество решающего правила измеряют частотой появления правильных решений. Обычно его оценивают, наделяя множество объектов Ω некоторой вероятностной мерой. Тогда задача записывается в виде min P .