Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Ферментативный катализ

Пример односторонней простой реакции первого порядка:

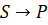
где S – субстрат (исходное вещество); Р - продукт.

В присутствии фермента реакция протекает по механизму Л. Михаэлиса:

k₁ k₂

S +E ↔ ES → P

k_-1

где E – фермент (энзим); ES – фермент-субстратный комплекс. Первая стадия – обратимая, быстрая; вторая – односторонняя, медленная.

Точного аналитического решения не существует, поэтому используется метод стационарных концентраций (Михаэлиса-Ментен). Скорость реакции определяется скоростью медленной стадии:

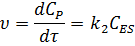
Скорость образования промежуточного вещества:

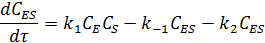
При условиях:

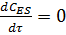· (концентрация фермент-субстратного комплекса стационарна);

· ;

· ;

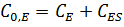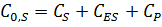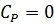· (в начальный момент времени отсутствует продукт);

· (начальная концентрация субстрата значительно выше начальной концентрации фермента) это означает, что мало и .

Концентрацию фермент-субстратного комплекса можно выразить уравнением:

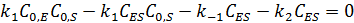
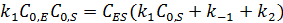
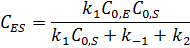
После деления числителя и знаменателя на 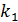получаем:

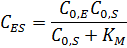
Величина 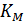– константа Михаэлиса (решение ИЮПАК) определяется выражением:

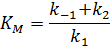
Уравнение скорости образования продукта в начальный момент времени:

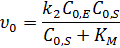
· Если 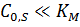, то можно записать:

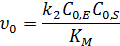
Начальная скорость линейно зависит от концентрации субстрата, порядок по субстрату первый, по ферменту – первый.

· Если , то получаем:

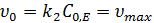
Начальная скорость не зависит от концентрации субстрата, порядок реакции по субстрату нулевой, по ферменту – первый. Скорость реакции достигает максимального значения, когда весь фермент насыщен субстратом. Именно в этих условиях удобно сравнивать скорости различных ферментативных реакций.

Для уравнения начальной скорости реакции можно записать:

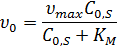
Зависимость скорости ферментативной реакции от времени представлена на рисунке.

Константа Михаэлиса 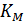численно равна концентрации субстрата, при которой активность фермента составляет половину максимальной:

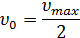
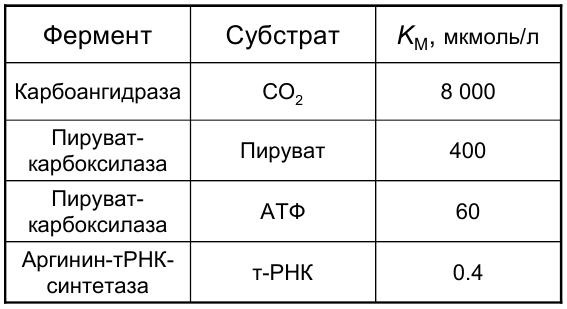
Величина 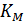имеет значения порядка 10^-2 -10^-8 моль/л и не зависит от концентрации фермента, а зависит от температуры, рН среды, активаторов и ингибиторов. 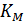характеризует специфичность фермента по отношению к субстрату (чем меньше 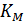, тем больше специфичность.

Если 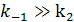то:

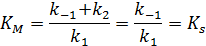
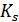– константа диссоциации фермент-субстратного комплекса, характеризует меру связывания фермента с субстратом, .

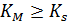Для ферментов с известной молекулярной массой и значением 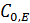можно рассчитать k₂:

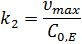
Величина k₂ – число оборотов – характеризует активность фермента (чем больше k₂, - тем выше активность).

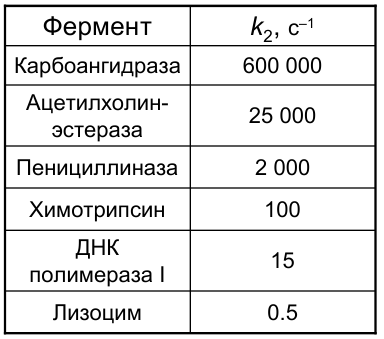
Для простых реакций если можно рассчитать k₁:
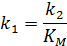