
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Положительно определенные квадратичные формы. Квадратичная форма от n переменных называется положительно определенной, если на любом ненулевом наборе значений переменных принимает положительные значения
|
|
Квадратичная форма от n переменных называется положительно определенной, если на любом ненулевом наборе значений переменных принимает положительные значения (AX, X)> 0 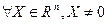
С помощью этого критерия нельзя по коэффициентам установить положительно определена ли квадратичная форма. Ответ на такой вопрос дает другая теорема, для формулировки которой введем еще одно понятие. Главные диагональные миноры матрицы A = (aij) – это миноры, расположенные в ее левом верхнем углу:
a 11, 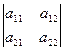 ,
, 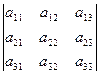 , …,
, …, 
Теорема. Квадратичная форма положительно определена тогда и только тогда, когда все ее главные диагональные миноры положительны.
Квадратичная форма от n переменных называется отрицательно определенной, если на любом ненулевом наборе значений переменных принимает отрицательные значения (AX, X)< 0 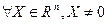
Теорема. Квадратичная форма отрицательно определена тогда и только тогда, когда ее главные диагональные миноры имеют чередующиеся знаки, начиная со знака минус.
|
|
