Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Фазовое равновесие

Фазовое равновесие – это равновесие процесса перехода вещества из одной фазы в другую (т. е. плавление, испарение, сублимация (возгонка), кристаллизация, конденсация, полиморфные превращения) без изменения химического состава системы. Например:

Твёрдое вещество		Жидкость;
Жидкость		Пар.

Как и химическое равновесие, фазовое равновесие является динамическим (скорости прямого и обратного процессов равны). Как и для химического равновесия, термодинамическим условием фазового равновесия является равенство энергии Гиббса нулю: D G_{P , T} = 0. Как и химическое равновесие, фазовое равновесие подчиняется закону действующих масс и принципу Ле Шателье – Брауна (см. выше).

Дадим определение некоторым основным понятиям, используемым в учении о фазовом равновесии. Компонент (составная часть системы) – каждое из содержащихся в системе химически однородных веществ, которое может быть выделено из неё и может существовать в изолированном виде длительное время. Например, водный раствор NaCl и KCl состоит из трёх компонентов: H₂O, NaCl и KCl.

Число независимых компонентов К – наименьшее число компонентов, достаточное как для образования всей системы, так и для образования любой из её фаз. К равно общему числу компонентов равновесной системы минус число уравнений, связывающих их концентрации при равновесии (химическом или фазовом). Например, в гетерогенной системе, находящейся в состоянии химического равновесия:

C(гр.) + CO₂(г.) «2CO(г.)

3 компонента (C(гр.), CO₂(г.), CO(г.)) и 2 независимых компонента, т. к. существует одно уравнение, связывающее концентрации компонентов системы в состоянии химического равновесия – уравнение константы химического равновесия (К = 3 – 1 = 2). Действительно, для образования всей данной системы и любой из её фаз достаточно двух компонентов: C(гр.) и CO₂(г.).

Число степеней свободы (вариантность) С – это число внешних условий (Т, Р, концентрация компонентов и т. д.), которые можно произвольно менять в некоторых пределах независимо друг от друга без изменения числа и вида равновесно сосуществующих фаз.

Одним из наиболее общих законов гетерогенного равновесия (химического и фазового) является правило фаз, выведенное в 1876 г. Дж.У. Гиббсом и использованное впервые на практике в 1889 г. Х. Розебомом. Согласно правилу фаз, в термодинамически равновесной системе числа степеней свободы С, фаз Ф, независимых компонентов К и внешних условий n, влияющих на равновесие, связаны соотношением:

Наибольшее влияние на фазовое равновесие оказывают 2 внешних условия: Р и Т. Поэтому обычно n = 2, и тогда правило фаз можно записать так:

Для однокомпонентной системы (К = 1) правило фаз имеет вид:

Для иллюстрации практического применения правила фаз рассмотрим простейший случай – диаграмму состояния однокомпонентной системы – воды (рис. 3.5). Данная диаграмма представляет собой совокупность следующих кривых, описывающих равновесное состояние двух фаз в координатах температура Т – давление Р:

1. ОС – кривая плавления. Характеризует зависимость температуры плавления льда от внешнего давления.

2. ОА – кривая сублимации (возгонки). Характеризует зависимость давления насыщенного пара льда от температуры.

3. ОК – кривая испарения. Характеризует зависимость давления насыщенного пара жидкой воды от температуры.

4. ОВ (изображена пунктиром). Характеризует зависимость давления насыщенного пара над переохлаждённой водой от температуры. ОВ описывает поведение воды в метастабильном состоянии (т. е. таком состоянии, когда имеются все признаки фазового равновесия, но D G_{P , T} ¹ 0). Например, воду можно охладить до температуры –72 °С при атмосферном давлении, не вызвав кристаллизации. Система может находиться в таком состоянии (метастабильном) неопределённо долгое время. Однако стоит внести в воду кристаллики льда или произвести перемешивание, начнётся быстрая кристаллизация с интенсивным выделением теплоты и повышением температуры до 0 °С. Система переходит в равновесное состояние.

Области, находящиеся между кривыми, являются однофазными областями (лёд, жидкость, пар). На диаграмме можно отметить следующие точки:

1. X – точка плавления льда при атмосферном давлении.

2. Y – точка кипения воды при атмосферном давлении.

3. О – тройная точка. В данной точке одновременно находятся в равновесии три фазы (лёд, жидкая вода, пар).

4. К – критическая точка. В данной точке исчезает различие между жидкостью и её паром. При температуре выше этой точки пары воды не могут быть превращены в жидкую воду никаким повышением давления, и вода переходит из парообразного состояния в газообразное (пар может находиться в равновесии с конденсированной фазой, а газ – нет). Вода (и любое другое вещество) при температуре выше критической точки также называется сверхкритическим флюидом (плотная текучая фаза, образующаяся при температурах и давлениях выше их критических значений [Эткинс, 2007]).

Для любой точки в однофазной области, например для точки Z (жидкость), по формуле (3.36) С = 3 – 1 = 2. Система является бивариантной, т. е. в некоторых пределах независимо друг от друга можно менять 2 внешних условия (Т и Р) без изменения числа и вида фаз.

Для любой точки, соответствующей двум равновесным фазам, например для точки X (лёд/жидкость), С = 3 – 2 = 1. Система является моновариантной, т. е. можно менять только одно внешнее условие (либо Т, либо Р) без изменения числа и вида фаз.

Наконец, для тройной точки О (лёд/жидкость/пар) С = 3 – 3 = 0. Система является нонвариантной (безвариантной), т. е. без изменения числа и вида фаз невозможно изменить ни одно из внешних условий.

Представленная на рис. 3.5. диаграмма состояния воды справедлива для низких давлений. В области высоких давлений лёд может существовать в нескольких кристаллических модификациях. Диаграмма выглядит гораздо сложнее [Киреев].

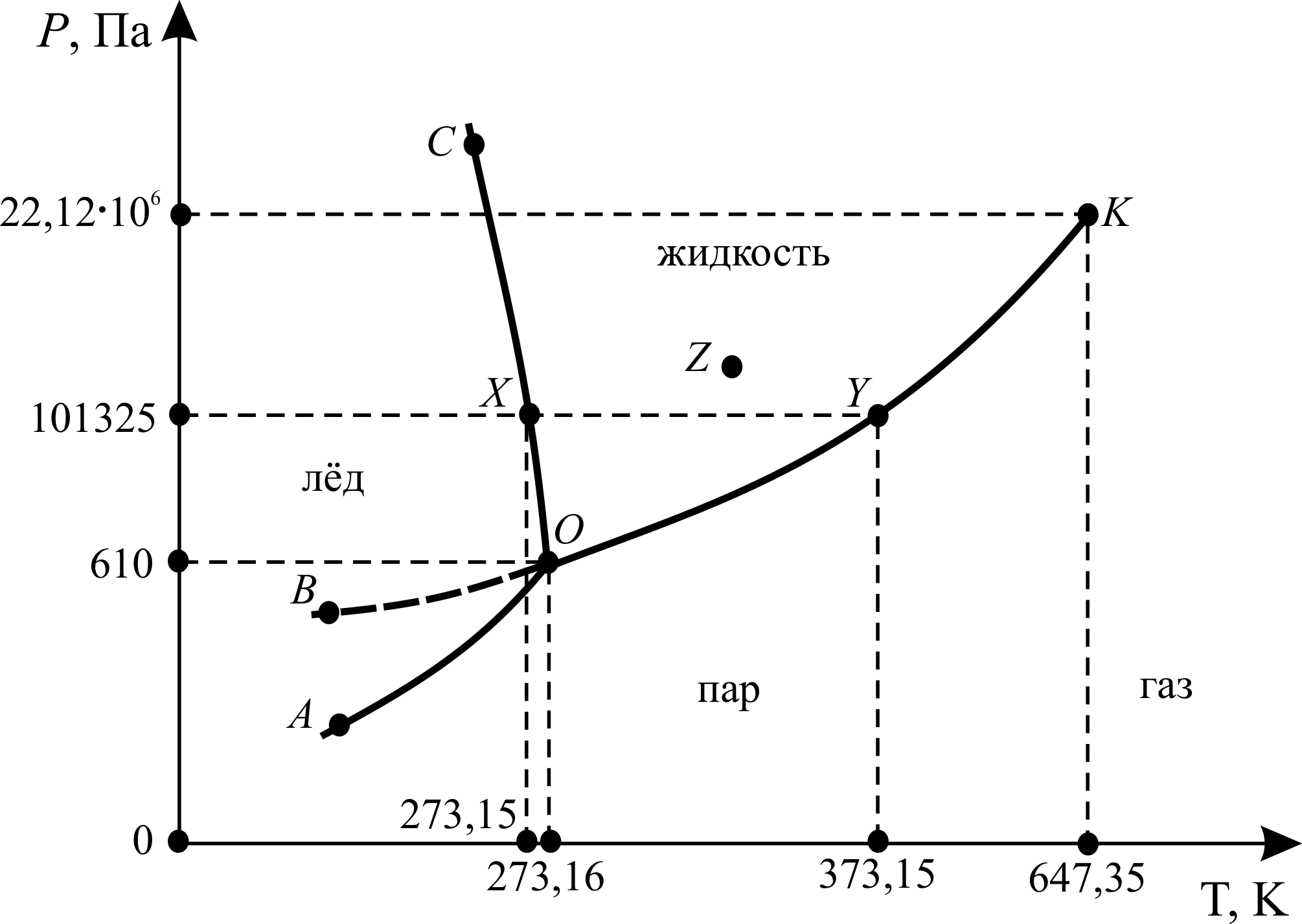
Рис. 3.5. Схема диаграммы состояния воды

[Равдель], [Справочник химика 1], [Эйзенберг]