
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Влияние концентрации на скорость реакции
|
|
ГЛАВА 3.
ХИМИЧЕСКАЯ КИНЕТИКА. РАВНОВЕСИЕ
Основные понятия химической кинетики. Скорость реакции
Влияние концентрации на скорость реакции
Влияние температуры на скорость реакции
Влияние катализаторов на скорость реакции
Химическое равновесие
Фазовое равновесие
Основные понятия химической кинетики. Скорость реакции
Химическая кинетика – это наука, изучающая закономерности протекания физико-химических процессов во времени. Химическая кинетика наравне с химической термодинамикой является теоретической основой химической технологии. Создание новых технологических процессов, расчёт оптимальных условий проведения реакций, конструирование и расчёт эффективных реакторов могут быть осуществлены успешно только с учётом законов химической кинетики. Рассмотрим основные понятия химической кинетики.
Элементарная (простая, одностадийная) химическая реакция – это реакция, протекающая путём прямого превращения молекул исходного вещества в молекулы продуктов реакций. Элементарных реакций меньшинство, в частности к ним относятся реакции диссоциации. Например:
H2 ® 2H или Cl2 ® 2Cl.
Элементарная химическая реакция является совокупностью множества протекающих за единицу времени однотипных элементарных химических актов.
Элементарный химический акт – это единичное взаимодействие частиц (молекул, атомов, ионов, радикалов), в результате которого образуются новые частицы продуктов реакции или промежуточных соединений.
Скорость элементарной химической реакции – это число однотипных элементарных химических актов, совершающихся в единицу времени в единице объёма (для гомогенных реакций) или на единице поверхности (для гетерогенных реакций) реакционного пространства при постоянном объёме системы или площади поверхности раздела фаз.
Сложная химическая реакция – это реакция, включающая несколько элементарных стадий химического превращения, протекающих последовательно или параллельно. Подавляющее большинство химических реакций являются сложными. Так, например, реакция:
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
H2 + I2 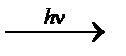 2HI 2HI
| (a) |
до определённого времени считалась элементарной. Теперь известно, что эта реакция сложная и включает следующие элементарные стадии:
I2 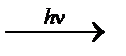 I· + I· I· + I·
| (b) | |
| I· + H2 ® HI + H· | (c) | |
| H· + I2 ® HI + I· | (d) | |
| I· + I· ® I2 | (e) |
(Для простоты изложения все четыре стадии реакции показаны, как практически односторонние.) При протекании сложной реакции возникают и расходуются промежуточные вещества. Обычно промежуточными веществами являются радикалы – активные частицы с неспаренными электронами. В реакции (а) промежуточными веществами являются радикалы I· и H·, возникающие на стадиях (b – d).
Механизм сложной химической реакции – это совокупность элементарных стадий, обеспечивающих протекание данного химического превращения. Механизм реакции (a) есть совокупность стадий (b – e). На основе механизма реакции можно получить закономерность (математическую модель), адекватно отражающую основные черты реального процесса.
Определить число элементарных химических актов, совершающихся при протекании химических реакций, невозможно. Поэтому скорость реакции количественно принято характеризовать изменением концентрации веществ – участников реакции в единицу времени.
Выделяют истинную (мгновенную) скорость реакции и среднюю скорость реакции. Истинная скорость реакции в данный момент времени u t – это изменение концентрации d C, относящееся к бесконечно малому промежутку времени dt:
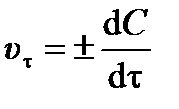 . .
| (3.1) |
Средняя скорость реакции за данный промежуток времени 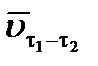 – это конечное изменение концентрации (С 2 – С 1), относящееся к промежутку времени (t2 – t1):
– это конечное изменение концентрации (С 2 – С 1), относящееся к промежутку времени (t2 – t1):
 . .
| (3.2) |
Скорость реакции всегда считается положительной. По существу безразлично, концентрацию какого из веществ – участников реакции рассматривать при расчёте скорости. Концентрация исходного вещества (реагента) будет уменьшаться, и тогда производная  и отношение
и отношение  будут отрицательны. Концентрация продукта реакции будет увеличиваться, тогда производная
будут отрицательны. Концентрация продукта реакции будет увеличиваться, тогда производная 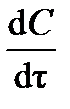 и отношение
и отношение 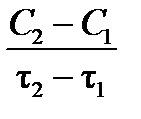 будут положительны. Поэтому, чтобы скорость имела положительное значение, в первом случае в правой части формул (3.1) и (3.2) ставится знак «–», во втором – знак «+».
будут положительны. Поэтому, чтобы скорость имела положительное значение, в первом случае в правой части формул (3.1) и (3.2) ставится знак «–», во втором – знак «+».
Единица измерения скорости реакции вытекает из выражения (3.1). Для гомогенной реакции (протекающей в объёме) изменение концентрации вещества ±d C можно выразить как отношение изменения количества вещества ±d n к объёму реакционного пространства V:
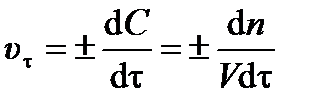 . .
| (3.3) |
Тогда единица измерения скорости в СИ 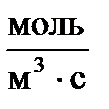 .
.
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.
Для новых пользователей первый месяц бесплатно. Зарегистрироваться в сервисе
Для гетерогенной реакции (протекающей на поверхности) изменение концентрации вещества ±d C можно выразить как отношение изменения количества вещества ±d n к площади поверхности раздела фаз s:
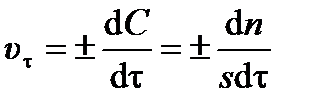 . .
| (3.4) |
Тогда единица измерения скорости в СИ 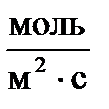 .
.
Рассмотрим определение скорости реакции на примере реакции термического разложения диацетилена:
НСº С–Сº СН(г.) 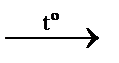 4С(графит) + Н2(г.).
4С(графит) + Н2(г.).
Данная реакция является гомогенной и односторонней (т. е. протекает до конца). На рис. 3.1 представлена кинетическая кривая реакции – графическая зависимость концентрации реагента С от времени t. Средняя скорость реакции за промежуток времени от t1 до t2 в соответствии с уравнением (3.2) определяется как:
 .
.
Истинная скорость реакции в момент времени t3 в соответствии с уравнением (3.1) может быть определена, как тангенс угла наклона касательной, проведённой к кинетической кривой в заданной точке:
 .
.
Экспериментальное определение скорости химической реакции заключается в определении изменения концентрации реагента или продукта реакции в единицу времени. Выделяют следующие методы определения изменения концентрации:
1. Химические методы. Например, в процессе реакции омыления этилацетата:
CH3–CO–O–C2H5 + NaOH ® CH3–CO–ONa + C2H5OH
можно определить изменение концентрации NaOH методом индикаторного титрования в присутствии фенолфталеина (бесцветный в кислой среде, пурпурный в щелочной).
2. Физико-химические методы. Например: определение изменения оптической плотности (оптический метод) или электропроводности (электрохимический метод) раствора в ходе реакции.
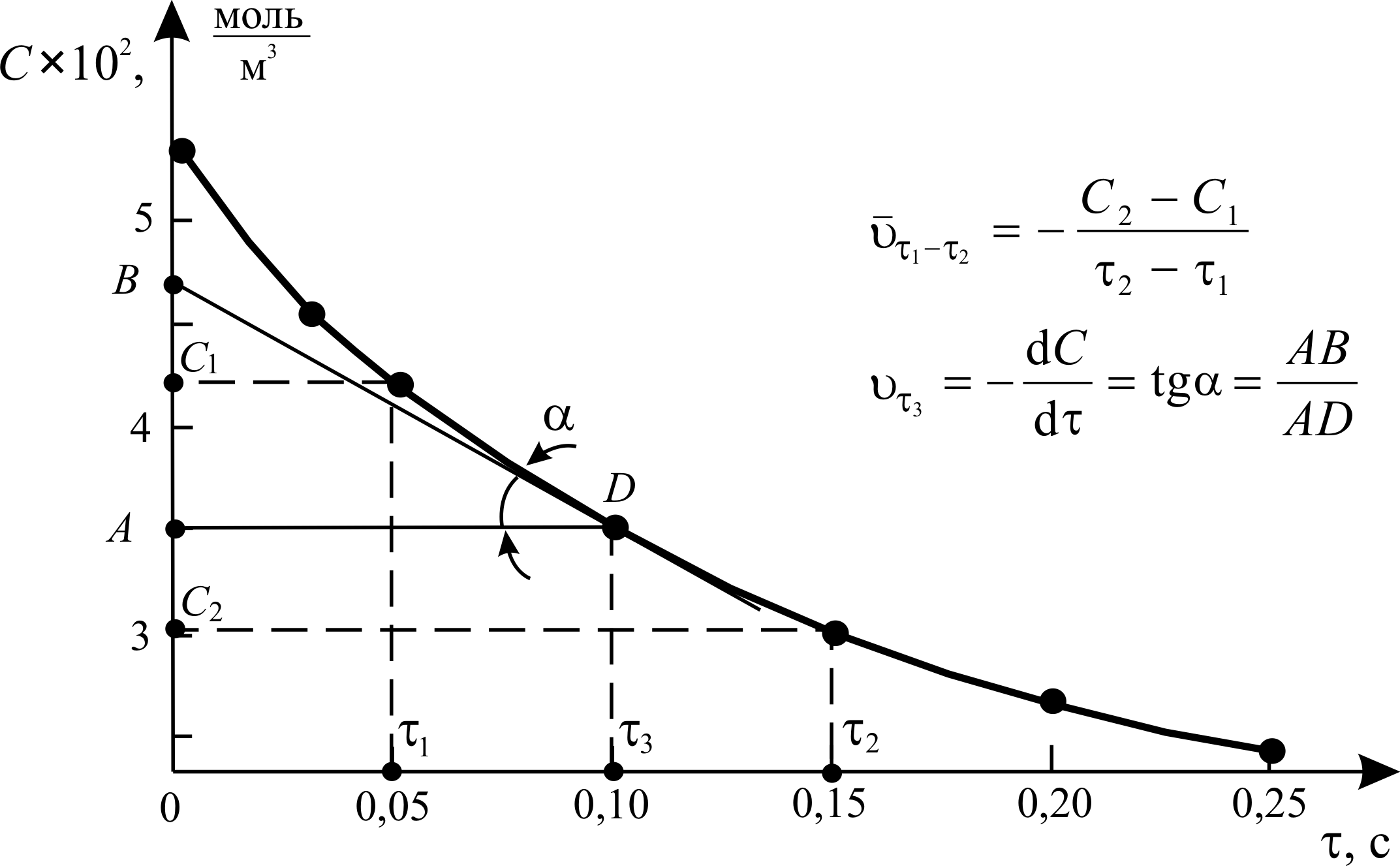
Рис. 3.1. Кинетическая кривая реакции термического разложения диацетилена.
Р = 1 атм, Т = 1173 К [Noggle, p.511]
На скорость химической реакции оказывают влияние следующие факторы:
- природа реагентов;
- концентрация реагентов;
- температура реакционной смеси;
- давление реакционной смеси (для реакций в газовой фазе);
- степень смешения реагентов (для гетерогенных реакций);
- природа растворителя (для реакций в растворе);
- присутствия катализаторов;
- воздействие различными видами энергии (механической, электрической, видимого, ультрафиолетового, инфракрасного, радиоактивного излучения).
Рассмотрим влияние на скорость химической реакции важнейших факторов.
Влияние концентрации на скорость реакции
Формальная кинетика химических реакций – это раздел химической кинетики, изучающий зависимость скорости реакции от концентрации реагентов. Задачей формальной кинетики является выяснение количественной связи между скоростью реакции и концентрацией реагентов в форме системы дифференциальных или интегральных (алгебраических) уравнений, а также установление механизма сложных химических реакций. В основе формальной кинетики лежит закон действующих масс.
Закон действующих масс(иначе – закон действия масс) был установлен в 1864 – 67 гг. К.М. Гульдбергом и П. Вааге. Его формулировка такова: скорость элементарной химической реакции пропорциональна произведению концентраций реагентов в степенях, равных стехиометрическим коэффициентам в уравнении реакции.
Для элементарной химической реакции, протекающей по схеме
| n1 А 1 + n2 А 2 ® Продукты | (3.5) |
закон действующих масс запишется в форме уравнения, обоснованного в 1867 г. Л. Пфаундлером с использованием законов молекулярно-кинетической теории:
 , ,
| (3.6) |
где С 1 – концентрация реагента А 1; С 2 – концентрация реагента А 2.
Сумма стехиометрических коэффициентов (n1 + n2) равна молекулярности реакции. Молекулярность реакции – это число частиц, участвующих в элементарном химическом акте. Молекулярность реакции – всегда целое положительное число: 1, 2, реже 3. В соответствии с этим выделяют моно-, би-, тримолекулярные реакции. Элементарных химических актов с одновременным участием четырёх (и большего количества) частиц не бывает, так как вероятность одновременного столкновения четырёх частиц ничтожно мала.
Коэффициент пропорциональности k в уравнении (3.6) называется константой скорости реакции. Константа k численно равна скорости реакции при концентрациях реагентов, равных единице. Константа скорости зависит от тех же факторов, что и скорость реакции (см. §3.1), за исключением концентрации реагентов.
Пример 3.1. Элементарная гомогенная химическая реакция между веществами А и В выражается уравнением:
А + 2 В ® Продукты.
Начальные концентрации составляют: С 0(А) = 0, 03  ; С 0(В) = 0, 05
; С 0(В) = 0, 05  . Константа скорости реакции равна 0, 4
. Константа скорости реакции равна 0, 4 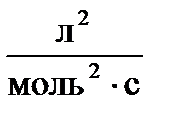 . Рассчитайте начальную скорость реакции u 0 и скорость реакции по истечении некоторого времени u 1, когда концентрация вещества А уменьшится на 0, 01
. Рассчитайте начальную скорость реакции u 0 и скорость реакции по истечении некоторого времени u 1, когда концентрация вещества А уменьшится на 0, 01  .
.
Решение:
1. u 0 рассчитаем по формуле (3.6):
u 0 = kС 0(А) С 0(В)2 = 0, 4 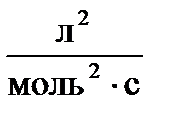 × 0, 03
× 0, 03  × (0, 05
× (0, 05  )2 = 3× 10–5
)2 = 3× 10–5  .
.
2. Если концентрация А уменьшилась на 0, 01  , то согласно уравнению реакции концентрация В должна уменьшится на 0, 02
, то согласно уравнению реакции концентрация В должна уменьшится на 0, 02  . Тогда, u 1 по формуле (3.6):
. Тогда, u 1 по формуле (3.6):
u 1 = kС 1(А) С 1(В)2 = 0, 4 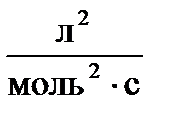 × (0, 03 – 0, 01)
× (0, 03 – 0, 01)  × (0, 05 – 0, 02
× (0, 05 – 0, 02  )2 =
)2 =
= 7, 2× 10–6  .
.
Ответ: u 0 = 3× 10–5  ; u 1 = 7, 2× 10–6
; u 1 = 7, 2× 10–6  .
.
Пример 3.2. Как изменится скорость протекающей в закрытом сосуде условно элементарной реакции:
2NO(г.) + O2(г.) ® 2NO2(г.),
если увеличить давление в 4 раза при постоянной температуре?
Решение:
Согласно уравнению Менделеева – Клапейрона (1.6) для газов в закрытой системе изотермическое увеличение давления прямо пропорционально увеличению концентрации. Тогда закон действующих масс (3.6) для данной реакции может быть записан в форме:
u = kP (NO)2 P (O2),
где P (NO) и P (O2) – парциальные давления NO и O2. Тогда изменение скорости реакции после увеличения давления в 4 раза: 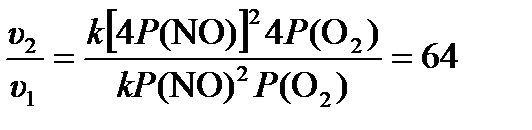 .
.
Ответ: 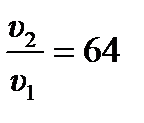 .
.
Сложные химические реакции включают несколько стадий, каждая из которых может быть моно-, би- или тримолекулярной. В сложных химических реакциях зависимость скорости от концентрации реагентов выражается более сложными уравнениями, чем (3.6), и закон действующих масс не может быть использован для описания химического превращения в целом. Однако, формально он часто используется и для сложных реакций в форме:
 , ,
| (3.7) |
где p 1 – порядок реакции по веществу А1; p 2 – порядок реакции по веществу А2.
Уравнение (3.7) называется кинетическим уравнением реакции и является математической моделью химической реакции.
Порядок реакции по данному веществу pi – это показатель степени концентрации данного вещества в кинетическом уравнении реакции. Для сложной реакции порядок по данному веществу pi не равен стехиометрическому коэффициенту данного вещества n i в уравнении реакции.
Общий или суммарный порядок реакции p – это сумма порядков реакции по всем реагентам. Для реакции (3.5) p = p 1 + p 2. В общем случае суммарный порядок меньше или равен молекулярности и может принимать целые (1, 2, 3) и дробные значения, а также быть равным нулю. Суммарный порядок реакции совпадает с молекулярностью только для элементарной реакции. Дробный суммарный порядок характерен для сложных реакций.
Реакции первого порядка (p = 1). К реакциям 1-го порядка относятся элементарные мономолекулярные реакции, протекающие по схеме
| А ® Продукты. | (3.8) |
Примерами таких реакций являются:
1. реакция термического разложения ряда веществ:
– диацетилена (см. §3.1);
– ацетона: СН3–СО–СН3 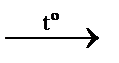 СО + С2Н6;
СО + С2Н6;
2. процессы радиоактивного распада (см. Пример 3.3).
Многие сложные реакции формально также можно отнести к первому порядку. Например:
1. реакция гидролитического разложения сахара в разбавленном водном растворе с образованием глюкозы и фруктозы (инверсия сахара):
С12Н22О11 + Н2О ® С6Н12О6 (глюкоза) + С6Н12О6 (фруктоза);
2. реакция гидролиза этилацетата в водной среде:
СH3–CO–O–C2H5 + Н2О ® CH3COOН + C2H5OH;
3. реакция разложения хлорида фенилдиазония в воде:
С6H5–N2Cl + H2O ® C6H5OH + H+ + Cl- + N2
В данных реакциях концентрация воды, находящейся в избытке, в ходе реакции остаётся практически постоянной. Такие реакции называются псевдомономолекулярными.
Дифференциальное кинетическое уравнение реакции первого порядка имеет вид
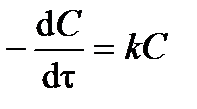 . .
| (3.9) |
Разделив переменные в уравнении (3.9) и проинтегрируем левую часть от начальной концентрации С 0 до концентрации С, а правую – от 0 до времени t, получим интегральное кинетическое уравнение реакции 1-го порядка:
 ; ; 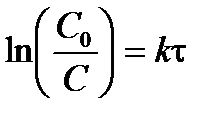 . .
| (3.10) |
Отсюда можно выразить константу скорости реакции первого порядка:
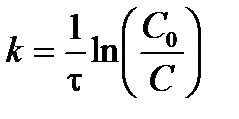 . .
| (3.11) |
Из выражения (3.11) следует, что константа скорости реакции первого порядка измеряется в  и не зависит от способа выражения концентрации.
и не зависит от способа выражения концентрации.
Для характеристики скорости реакции наряду с константой скорости часто используют величину, называемую периодом полураспада. Период полураспада (время половинного превращения) t1/2 – это время, за которое начальная концентрация исходного вещества уменьшается в 2 раза. Подставив в уравнение (3.10) С 0/2 вместо С и t1/2 вместо t, получим выражение для периода полураспада реакции первого порядка:
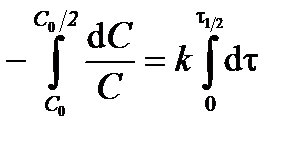 ; ;  ; ;  . .
| (3.12) |
Из выражения (3.12) следует, что период полураспада реакции первого порядка не зависит от начальной концентрации реагирующего вещества С 0.
Пример 3.3. Период полураспада радиоактивного изотопа 14С t1/2 = 5730 лет. При археологических раскопках было найдено дерево содержание 14С в котором составляло 72 % от нормального. Каков возраст дерева? *
Решение:
Из формулы (3.12) выразим константу скорости реакции радиоактивного распада:
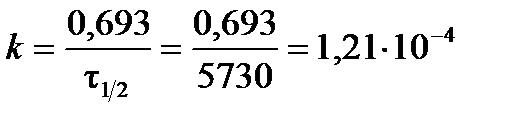 год–1.
год–1.
Из формулы (3.11) выразим возраст дерева (т. е. время t):
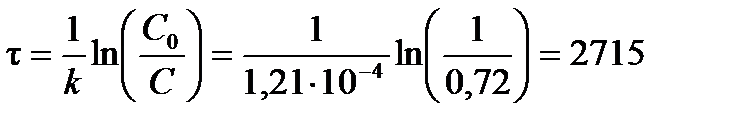 лет.
лет.
Ответ: возраст дерева 2715 лет.
*Радиоактивность изотопа 14С обусловлена β -распадом:
 .
Радиоуглеродный метод геохронологии разработал в 1946 г. У.Ф. Либби. Метод широко используется для датировки образцов, имеющих возраст вплоть до 35000 лет. Точность метода – приблизительно 300 лет. Наилучшие результаты получаются при определении возраста шерсти, семян, ракушек и костей. Для определения возраста образца измеряют активность β -излучения (число распадов в минуту) в расчёте на 1 г, содержащегося в нём углерода. Это позволяет установить возраст образца при помощи кривой радиоактивного распада для изотопа .
Радиоуглеродный метод геохронологии разработал в 1946 г. У.Ф. Либби. Метод широко используется для датировки образцов, имеющих возраст вплоть до 35000 лет. Точность метода – приблизительно 300 лет. Наилучшие результаты получаются при определении возраста шерсти, семян, ракушек и костей. Для определения возраста образца измеряют активность β -излучения (число распадов в минуту) в расчёте на 1 г, содержащегося в нём углерода. Это позволяет установить возраст образца при помощи кривой радиоактивного распада для изотопа  . [Фримантл 1, 58] . [Фримантл 1, 58]
|
Пример 3.4. Константа скорости для реакции первого порядка:
SO2Cl2 ® SO2 + Cl2
k = 2, 2× 10–5  при температуре 320 °С. Какой процент SO2Cl2 разложится при выдерживании его в течение 2 часов при данной температуре.
при температуре 320 °С. Какой процент SO2Cl2 разложится при выдерживании его в течение 2 часов при данной температуре.
Решение:
Примем начальную концентрацию SO2Cl2 С 0 = 100, а концентрацию через 2 ч (7200 с) разложения С = 100 – x, где x – процент разложившегося SO2Cl2. Тогда уравнение (3.11) примет вид:
 .
.
Отсюда:

Ответ: через 2 ч разложится 14, 65 % SO2Cl2.
Реакции второго порядка (p = 2). К реакциям 2-го порядка относятся элементарные бимолекулярные реакции, протекающие по схеме:
| А 1 + А 2 ® Продукты. | (3.13) |
Примерами формально бимолекулярных реакций являются:
1. реакция омыления сложного эфира (см § 3.1);
2. реакция образования галогеноводорода в газовой фазе: H2(г.) + I2(г.) ® 2HI(г.);
3. реакция этерификации: CH3COOH + C2H5OH ® СH3–CO–O–C2H5.
Для реакции второго порядка дифференциальное кинетическое уравнение имеет вид:
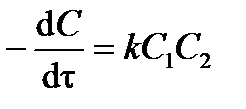 . .
| (3.14) |
В простейшем случае, когда концентрации двух реагирующих веществ являются одинаковыми (или когда реагент один), т. е.: С 1 = С 2 = С, уравнение (3.14) примет вид:
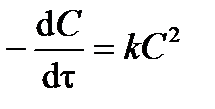 . .
| (3.15) |
Разделив переменные в уравнении (3.15) и проинтегрируем левую часть от С 0 до С, а правую – от 0 до t, получим интегральное кинетическое уравнение реакции второго порядка:
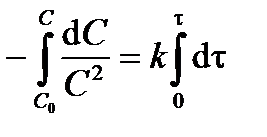 ; ;  . .
| (3.16) |
Отсюда можно выразить константу скорости реакции 2-го порядка (для С 1 = С 2):
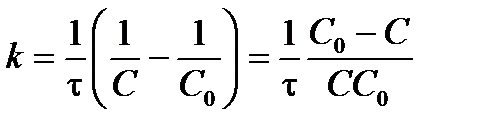 . .
| (3.17) |
Из выражения (3.17) следует, что константа скорости реакции 2-го порядка (а также и более высоких порядков) зависит от способа выражения концентрации. Если концентрация реагента выражена в  (гомогенная реакция), то константа скорости реакции второго порядка измеряется в
(гомогенная реакция), то константа скорости реакции второго порядка измеряется в  .
.
Подставив в уравнение (3.16) С 0/2 вместо С и t1/2 вместо t, получим выражение для периода полураспада реакции второго порядка (для С 1 = С 2):
 ; ; 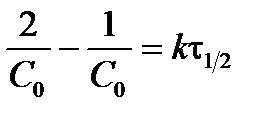 ; ;  . .
| (3.18) |
Из выражения (3.18) следует, что период полураспада реакции второго порядка (и более высоких порядков) зависит от начальной концентрации реагирующего вещества С 0.
Пример 3.5. Установлено, что реакция второго порядка (с одним реагентом) завершается на 75 % за 92 мин при исходной концентрации реагента С 0 = 0, 24  . Какое время потребуется, чтобы при тех же условиях концентрация реагента С достигла 0, 16
. Какое время потребуется, чтобы при тех же условиях концентрация реагента С достигла 0, 16  .
.
Решение:
Если реакция прошла на 75 %, то концентрация реагента С = (1 – 0, 75) С 0 = 0, 25 С 0.
Константу скорости реакции рассчитаем по формуле (3.17):
 .
.
Из формулы (3.17) выразим время t, необходимое для достижения С реагента 0, 16  :
:

 мин.
мин.
Ответ: t = 15, 3 мин.
Порядок и константу скорости реакции можно определить дифференциальным способом (предложен в 1884 г. Я.Х. Вант-Гоффом). Способ заключается в следующем. По кинетической кривой (см. рис.3.1) определяют истинную скорость реакции 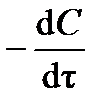 в разные моменты времени t. Получают зависимость
в разные моменты времени t. Получают зависимость 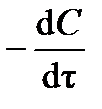 от концентрации реагента С. Логарифмируя дифференциальное кинетическое уравнение реакции n -го порядка:
от концентрации реагента С. Логарифмируя дифференциальное кинетическое уравнение реакции n -го порядка:
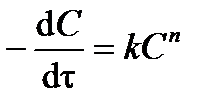 , ,
| (3.19) |
получают линейное уравнение:
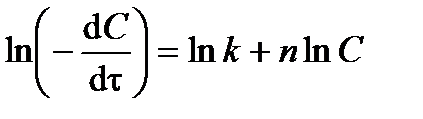 . .
| (3.20) |
На графике в координатах 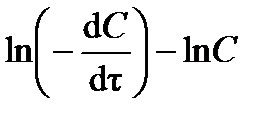 точки должны расположиться на прямой линии (рис.3.2). Следовательно, тангенс угла наклона прямой будет равен порядку реакции (tga = n), а отрезок, отсекаемый прямой на оси ординат – логарифму константы скорости реакции (0 A = ln k).
точки должны расположиться на прямой линии (рис.3.2). Следовательно, тангенс угла наклона прямой будет равен порядку реакции (tga = n), а отрезок, отсекаемый прямой на оси ординат – логарифму константы скорости реакции (0 A = ln k).

| Рис. 3.2.Схема графического определения порядка n константы скорости реакции k |
|
|
