💸 Как сделать бизнес проще, а карман толще?

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое раписание, но и напоминать клиентам о визитах тоже. Проблема в том, что средняя цена по рынку за такой сервис — 800 руб/мес или почти 15 000 руб за год. И это минимальный функционал. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
⚡️ Для новых пользователей первый месяц бесплатно. А далее 290 руб/мес, это в 3 раза дешевле аналогов. За эту цену доступен весь функционал: напоминание о визитах, чаевые, предоплаты, общение с клиентами, переносы записей и так далее.
✅ Уйма гибких настроек, которые помогут вам зарабатывать больше и забыть про чувство «что-то мне нужно было сделать».
Сомневаетесь? нажмите на текст, запустите чат-бота и убедитесь во всем сами!

Then begin. NextNode^.Visited:=True; // то отметка его как посещенного,

NextNode^.Visited: =True; // то отметка его как посещенного,

Write(f, NextNode^.Value, ' > '); // посещение узла

q.Insert(NextNode); // и включение его в конец очереди

end;

Arc: =Arc^.NextArc; // переход к следующему смежному с Node узлу

end;

end;

Writeln(f); q.Free; // удаление очереди

end; // procedure BFS

Для графа

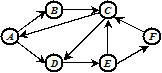
обход в глубину дает последовательность узлов A, B, C, D, E, F, обход в ширину – A, B, D, C, E, F.

Если некоторые узлы графа при поиске от начального узла остались непосещенными, то выбирается один из них и поиск повторяется. Этот процесс продолжается до тех пор, пока обходом не будут охвачены все узлы графа.

6. Вычисление расстояния между узлами ориентированного графа

Напомним, что расстоянием между двумя узлами n1 и n2 называется длина кратчайшего пути между этими узлами. Очевидно, что представляет интерес не только значение расстояния между двумя узлами, но и перечень узлов, входящих в кратчайший путь. Для решения этой задачи необходимо переопределить тип tNode, включив в него дополнительные поля: Dist – расстояние до данного узла от некоторого другого узла, PrevNode – указатель на узел, предшествующий текущему в кратчайшем пути. Начальное значение поля Dist для всех узлов равно нулю. Определяем расстояния от узла n1 до всех остальных узлов графа, для чего последовательно обходим граф от узла n1 по спискам смежности и в поле Dist узла, являющегося концом очередной дуги, записываем значение, равное сумме уже вычисленного расстояния до начального узла дуги плюс 1. Изменять значение поля Dist конечного узла дуги надо только в том случае, если оно меньше того значения, которое в этом поле хранится (расстояние – длина кратчайшего пути до узла). При каждом изменении значения поля Dist необходимо переопределять значение поля PrevNode, записывая в него указатель на тот узел, длина пути от которого до текущего узла оказалась меньшей.

Дополнительно необходимо хранить сведения об уже пройденных узлах (можно использовать поле Visited логического типа), чтобы не посещать их повторно. Начальное значение этого поля для всех узлов равно False. В основе алгоритма вычисления кратчайшего пути между узлами n1 и n2 лежит рекурсивный обход графа в глубину.

Метод tOrGraph.SPath возвращает строку с перечнем информационных полей узлов графа (типа tValue=Char), входящих в кратчайший путь между узлами Node1 и Node2. Длина кратчайшего пути (расстояние) равна длине этой строки, уменьшенной на 1.

function tOrGraph.SPath(Node1, Node2: pNode): String;

// Кратчайший путь между узлами Node1 и Node2

procedure PathFromNode(Node: pNode);

// Внутренняя рекурсивная процедура

// вычисления расстояния от узла Node до всех узлов графа

Var

Arc: pArc; // дуга графа

NextNode: pNode; // узел графа, следующий за Node

Begin

Node^.Visited: =True; // отметка о посещении узла Node

Arc: =Node^.ArcList; // указатель на список смежности узла Node

while Arc< > nil do begin // пока не исчерпан список смежности узла Node

NextNode: =Arc^.RearNode; // узел, смежный с узлом Node

if not NextNode^.Visited

then begin // если узел NextNode еще не посещался,

NextNode^.Dist: =Node^.Dist+1; // то расстояние до него равно 1,

PathFromNode(NextNode); // продолжаем обход от него

NextNode^.PrevNode: =Node; // предыдущий узел для NextNode - Node

End

else // если узел NextNode уже посещался и,

if Node^.Dist+1< NextNode^.Dist // длина пути к нему через узел Node меньше