
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Оценка генерального среднего с помощью критерия Стьюдента
|
|
Предполагается, что наблюдаемая случайная величина имеет нормальное распределение. Для оценки генерального среднего желательно знать генеральную дисперсию s2. Но ее нельзя найти из наблюдений и вместо нее обычно берут выборочную дисперсию S 2.
Вводят величину
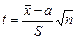 ,
,
где 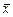 – выборочное среднее; S 2 – выборочная дисперсия; а – генеральное среднее; n – объем выборки.
– выборочное среднее; S 2 – выборочная дисперсия; а – генеральное среднее; n – объем выборки.
Таким образом, величина t – это не что иное, как нормированное отклонение 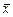 от а.
от а.
Функция распределения величины t называется t –распределением, или распределением Стьюдента. Она зависит только от числа f степеней свободы, по которым подсчитана дисперсия S 2. Если дисперсия S 2 и среднее 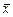 подсчитывались по одним и тем же наблюдениям, то f = n - 1. Плотность j(t) распределения Стьюдента имеет вид:
подсчитывались по одним и тем же наблюдениям, то f = n - 1. Плотность j(t) распределения Стьюдента имеет вид:
По форме графики напоминают плотность нормального распределения, но при t ® ±¥ они значительно медленнее сближаются с осью абсцисс.
Представляет интерес рассмотрение одной из числовых характеристик случайной величины, которую называют квантиль.
Квантилем хр случайной величины Х с функцией распределения F (x) называют решение уравнения
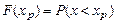 ,
,
где вероятность Р – заданная величина.
Величины квантилей представлены в специальных таблицах для соответствующих значений вероятности Р.
Возвращаясь к распределению Стьюдента, обозначим tp – квантиль t –распределения.
Если 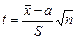 , то известно, что доверительные границы генерального среднего могут быть определены из двусторонних неравенств
, то известно, что доверительные границы генерального среднего могут быть определены из двусторонних неравенств
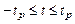 или
или 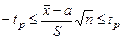 .
.
Преобразуем поэтапно двустороннее неравенство. Для этого:
1) Берем левую границу:
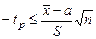 ;
; 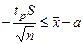 ;
;
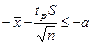 ; откуда
; откуда 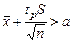 .
.
2) Рассматриваем правую границу:
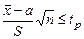 ;
; 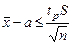 ;
;
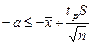 ; или, в итоге
; или, в итоге 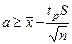 .
.
Окончательно получаем:
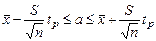 ,
,
что можно представить в виде:
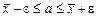 .
.
Таким образом, с вероятностью р – генеральное значение математического ожидания заключается в границах между 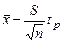 и
и 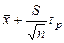 , где величина tр определяется по таблицам распределения Стьюдента для заданной доверительной вероятности р и определяемого числа степеней свободы f = n
, где величина tр определяется по таблицам распределения Стьюдента для заданной доверительной вероятности р и определяемого числа степеней свободы f = n 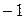 .
.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
Распределение Стьюдента позволяет оценивать генеральное среднее (математическое ожидание), когда генеральная дисперсия неизвестна. При этом число наблюдений может быть очень малым, даже равным двум. Конечно, скудость информации сказывается на результатах – доверительные границы получаются довольно широкими. Поэтому везде, где это только возможно, нужно стараться увеличивать число степеней свободы у выборочной дисперсии.
Доверительные интервалы и доверительные вероятности
Выборочные параметры могут служить приближенными оценками соответствующих генеральных параметров. Погрешность такой оценки, как об этом говорилось ранее, тем меньше, чем больше объем выборки. Как можно оценить эту погрешность более строго?
Все выборочные параметры (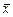 , S 2) являются случайными величинами и их отклонения от генеральных параметров (погрешности) также будут случайными. Поэтому вопрос об оценке этих отклонений носит вероятностный характер и можно лишь указать вероятность той или иной погрешности, т.е. найти вероятность того, что некоторая случайная величина Dn (отклонение выборочного параметра n от исследуемого генерального) не превосходит по абсолютной величине некоторого заданного числа e. Задача легко решается, если известны функции распределения F (x) или j(х) величины Dn.
, S 2) являются случайными величинами и их отклонения от генеральных параметров (погрешности) также будут случайными. Поэтому вопрос об оценке этих отклонений носит вероятностный характер и можно лишь указать вероятность той или иной погрешности, т.е. найти вероятность того, что некоторая случайная величина Dn (отклонение выборочного параметра n от исследуемого генерального) не превосходит по абсолютной величине некоторого заданного числа e. Задача легко решается, если известны функции распределения F (x) или j(х) величины Dn.
Известно:
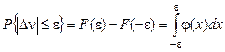 .
.
Но, к сожалению, обычно и F (x), и j(х) неизвестны.
Задачу решают по другому. Находят с заданной вероятностью границы возможных значений изучаемого параметра. Эту заданную вероятность называют доверительной вероятностью. В зависимости от конкретных обстоятельств в качестве доверительной вероятности берут р = 0, 95; 0, 98; 0, 99; реже р = 0, 90 или р = 0, 999.
Иногда вместо доверительной вероятности рассматривают связанную с ней величину – так называемый уровень значимости a=1 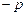 .
.
Соответствующие доверительной вероятности границы значений параметра называют доверительными границами, а образуемый ими интервал – доверительным интервалом.
Представляет интерес оценка генерального среднего и генеральной дисперсии с точки зрения определения их доверительных границ.
Стационарные случайные процессы
.Особое место занимают стационарные случайные процессы. Для них вид функции распределения вероятности не зависит от смещения начала отсчета вдоль оси времени. В случае стационарных случайных процессов определение функции распределения упрощается в том отношении, что она может быть определена в течение достаточно долгого промежутка времени из результатов наблюдения над одной единственной системой, а не над многими. Действительно, так как в этом случае функция распределения не зависит от начала отсчета времени, то можно предположить, что экспериментальную запись кривой х (t), полученную из наблюдения над одной системой в течение достаточно долгого промежутка времени, можно разбить на ряд отрезков длиной Т (где Т велико по сравнению со всеми «периодами», которые имеются в исследуемом процессе) и считать, что функциями, входящими в совокупность, являются функции х (t), представляющие собой части всей кривой х (t) на протяжении каждого из отрезков Т.
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.
Для новых пользователей первый месяц бесплатно. Зарегистрироваться в сервисе
В основе этого предположения лежит так называемая эргодическая гипотеза, согласно которой большое число наблюдений над одной – единственной системой, движение которой представляет собой стационарный случайный процесс, в моменты времени, выбранные произвольным образом, имеет те же статистические свойства, то же число наблюдений над произвольно выбранными подобными ей системами в один и тот же момент времени.
Различают «среднее значение по совокупности (множеству)», т.е. средние значения, определенные на основании наблюдения над многими подобными системами в один и тот же момент времени, и «среднее по времени», т.е. среднее значение, определенное на основании наблюдения над одной из этих систем для достаточно большого числа последующих моментов времени.
Для стационарных процессов это одно и то же. Так, например, для функции х (t) «среднее по совокупности» 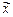 :
:
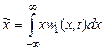 – зависит от момента времени t, а среднее по времени
– зависит от момента времени t, а среднее по времени 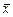 для интервала времени 2 Т:
для интервала времени 2 Т:
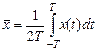 – не зависит от t и для стационарного процесса
– не зависит от t и для стационарного процесса 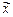 =
= 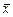 .
.
Аналогичное равенство имеет место и для моментов более высокого порядка.
Множественная линейная регрессия
Обозначим через Х 1 и Х 2 независимые переменные, а через У – зависимую случайную величину. Их реализации будут соответственно: х 1i, x 2i, y i (i = 1, 2, …, m), если m – объем выборки. Предположим, что случайная величина У для любой фиксированной пары значений (х 1; х 2) распределена по нормальному закону.
Уравнение регрессии ищем в виде
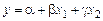 .
.
Оценки для коэффициентов a, b и g получаем, используя метод наименьших квадратов, т.е. обеспечивается выполнение условий:
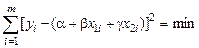 .
.
Приравняв нулю частные производные по a, b и g, получим систему линейных уравнений для определения a, b и g:
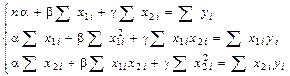 .
.
Преобразование этой системы с учетом обозначений
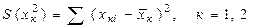
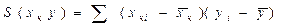
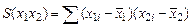
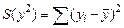
дает оценки коэффициентов a, b, g:
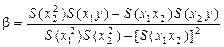 ,
,
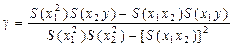 ,
,
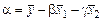 .
.
Коэффициенты b и g являются коэффициентами регрессии(множественные коэффициенты регрессии).
Величина b показывает зависимость значений у от значений х 1 при постоянном х 2. Поэтому иногда используют обозначение b = 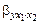 . Соответственно (g =
. Соответственно (g = 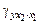 ) выражает зависимость значений у от значений х 2 при постоянном х 1.
) выражает зависимость значений у от значений х 2 при постоянном х 1.
Уравнение плоскости регрессии получают в виде 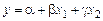 . Оно имеет смысл лишь в определенной области изменения значений х 1 и х 2.Аналогично – при большем количестве х.
. Оно имеет смысл лишь в определенной области изменения значений х 1 и х 2.Аналогично – при большем количестве х.
|
|
