Элементы операционного исчисления. Преобразование Лапласа

Под операционным исчислением понимается совокупность методов прикладного математического анализа, позволяющих экономными и непосредственно ведущими к цели средствами получать решения линейных дифференциальных уравнений. Операционное исчисление нашло широкое применение в теории автоматического управления, где с его помощью производится анализ переходных и установившихся процессов в автоматических системах.

Понятие оператора является обобщением понятия функции. Функция – закон соответствия между двумя множествами чисел. Оператор – это закон соответствия между двумя множествами функций. Этот закон может быть задан, например, таблицей, где каждой функции f (t) из определенного класса соответствует какая–либо иная функция F (p). Закон соответствия может быть записан следующим образом: f (t) ® F (p). (Стрелка означает «соответствует»).

В операционном исчислении рассматриваются операторы, заданные некоторой частной формулой преобразования. Так, пусть задана некоторая функция f (t) действительной переменной t, причем такая, что для нее существует преобразование Лапласа (L –преобразование)

.

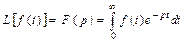Используя L –преобразование, можно каждой преобразуемой по Лапласу функции f (t) (в этом случае функция f (t) называется «оригиналом») поставить в соответствие функцию F (p) комплексной переменной р = с + j w (при этом функция F (p) называется «изображением» функции f (t)).

Преобразование Лапласа обладает рядом замечательных свойств. Например, дифференцированию оригинала f (t) по переменной t соответствует операция умножения изображения F (p) на комплексную переменную р, а интегрированию оригинала f (t) соответствует операция деления F (p) на р. Таком образом, операции дифференцирования и интегрирования оригинала заменяются в пространстве изображений оригинала более простыми операциями алгебры – соответственно умножением и делением изображения F (p) на р. Это позволяет дифференциальное уравнение, записанное относительно искомой функции f (t), заменить в пространстве изображений на алгебраическое уравнение относительно изображения F (p)= L [ f (t)]. Решив это алгебраическое уравнение и найдя F (p), мы получим изображение решения исходного дифференциального уравнения. Для определения самого решения можно воспользоваться обратным преобразованием Лапласа (L ^–1–преобразованием), устанавливающим связь между изображением F (p) и оригиналом f (t):

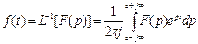, t > 0

где с = R ep.

Функция f (t) может считаться оригиналом, если выполняются следующие условия:

1) Функция f (t) непрерывна для всех значений t ³ 0. Непрерывность может быть нарушена лишь в отдельных точках, являющихся точками разрыва непрерывности первого рода, причем число этих точек должно быть конечным на любом интервале ограниченной длины.

2) Функция f (t) = 0 для значений t < 0.

3) Функция f (t) имеет ограниченный порядок возрастания, т.е. можно указать такие постоянные числа М > 0 и с _о ³ 0, при которых выполняется неравенство 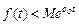(t > 0).

Стационарные случайные процессы

.

Особое место занимают стационарные случайные процессы. Для них вид функции распределения вероятности не зависит от смещения начала отсчета вдоль оси времени. В случае стационарных случайных процессов определение функции распределения упрощается в том отношении, что она может быть определена в течение достаточно долгого промежутка времени из результатов наблюдения над одной единственной системой, а не над многими. Действительно, так как в этом случае функция распределения не зависит от начала отсчета времени, то можно предположить, что экспериментальную запись кривой х (t), полученную из наблюдения над одной системой в течение достаточно долгого промежутка времени, можно разбить на ряд отрезков длиной Т (где Т велико по сравнению со всеми «периодами», которые имеются в исследуемом процессе) и считать, что функциями, входящими в совокупность, являются функции х (t), представляющие собой части всей кривой х (t) на протяжении каждого из отрезков Т.

В основе этого предположения лежит так называемая эргодическая гипотеза, согласно которой большое число наблюдений над одной – единственной системой, движение которой представляет собой стационарный случайный процесс, в моменты времени, выбранные произвольным образом, имеет те же статистические свойства, то же число наблюдений над произвольно выбранными подобными ей системами в один и тот же момент времени.

Различают «среднее значение по совокупности (множеству)», т.е. средние значения, определенные на основании наблюдения над многими подобными системами в один и тот же момент времени, и «среднее по времени», т.е. среднее значение, определенное на основании наблюдения над одной из этих систем для достаточно большого числа последующих моментов времени.

Для стационарных процессов это одно и то же. Так, например, для функции х (t) «среднее по совокупности» :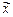

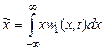– зависит от момента времени t, а среднее по времени 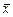для интервала времени 2 Т:

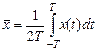– не зависит от t и для стационарного процесса = .

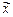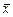Аналогичное равенство имеет место и для моментов более высокого порядка.

Случайные процессы

Функция, значение которой при каждом данном значении независимой переменной является случайной величиной, называется случайной функцией. То есть, это бесконечная совокупность случайных величин, зависящая от непрерывно изменяющейся независимой переменной. Случайная функция, зарегистрированная по результатам опыта, называется реализацией случайной функции. Случайная функция, для которой независимой переменной является время t называется случайным (стохастическим) процессом.

Для характеристики случайной функции служат моменты случайной функции. Для их определения необходимо знать многомерные функции распределения случайной величины.

Предположим, что мы располагаем большим числом однотипных систем, работающих одновременно при одинаковых условиях. Будем наблюдать изменения величин на выходе этих устройств. Они будут характеризоваться некоторыми случайными функциями 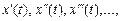причем все эти функции будут отличаться друг от друга.

Рассмотрим какой–либо момент времени t и найдем, какая доля из общего числа функций x(t) имеет в этот момент времени значение, заключенное между х и x + dx.

Эта доля зависит от момента времени t и пропорциональна dx при малых dx. Обозначим ее через w ₁(х, t) dx – (при количестве реализаций, стремящихся к бесконечности, эта величина соответствует вероятности того, что в момент времени t величина х будет заключена в пределах х и х + d х) и назовем w ₁(х, t) – первой или одномерной функцией распределения вероятности.

Рассмотрим теперь все возможные пары значений х, наблюденные в два различных момента времени t ₁ и t ₂. Долю пар значений х, для которой величина х заключена между (х ₁, х ₁+ d х ₁) при t = t ₁ и между (х ₂, х ₂ + d х ₂) при t = t ₂, отнесенную к общему числу наблюденных пар значений, обозначим через w ₂(х ₁, t ₁, х ₂, t ₂)d x ₁d x ₂ и назовем второй или двумерной функцией распределения вероятности.

Этот процесс можно продолжить и определить третью, четвертую и все последующие функции распределения вероятности.

Итак, случайный процесс можно характеризовать некоторыми функциями распределения вероятности, полностью определяющими его в статистическом смысле.

Действительно, зная w ₁(х, t) можно определить математическое ожидание m _{o x} (t) случайной величины х (t):

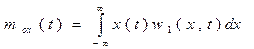
и его дисперсию b_{2 х} (t):

.

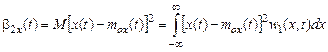Зная вторую функцию распределения w ₂(х ₁, t ₁, х ₂, t ₂), можно определить как m _ox(t), b_2х(t), так и центральный момент 2–го порядка:

,

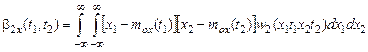характеризующий связь между значениями случайной функции в различные моменты времени. Функция b_2х(t ₁, t ₂) называется корреляционной функцией.

Зная n –мерную функцию распределения вероятности, можно определить все последующие моменты случайной функции, включая момент n –го порядка.

Если приходится иметь дело не с одной, а с несколькими взаимосвязанными функциями, то кроме их собственных моментов, приходится вводить еще и их взаимные моменты.

Так, например, если имеются две случайные функции х (t) и y (t), то простейшим взаимным моментом является момент 2–го порядка:

=

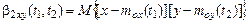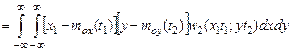
называемый взаимной корреляционной функцией случайных процессов х (t) и y (t).

Гипотеза о равенстве дисперсий. Критерий Фишера

Сравнение двух или нескольких выборочных дисперсий является одной из важнейших задач статистической обработки наблюдений. Основной выясняемый вопрос при этом – можно ли считать сравниваемые выборочные дисперсии оценками одной и той же генеральной дисперсии.

Начнем со сравнения двух выборочных дисперсий и 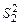, имеющих соответственно f ₁ и f ₂ степеней свободы. Будем считать, что первая выборка сделана из генеральной совокупности с дисперсией 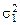, вторая – из генеральной совокупности с дисперсией 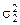. Выдвигается нулевая гипотеза – гипотеза о равенстве генеральных дисперсий 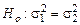. Для того, чтобы отвергнуть эту гипотезу, нужно доказать значимость расхождения между и 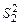при выбранном уровне значимости a = 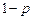. В качестве критерия значимости обычно используется так называемое распределение Фишера.

Распределением Фишера (или F –распределением) называется распределение случайной величины:

.

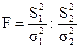Это распределение зависит только от f ₁ и f ₂ при этом 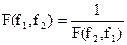.