Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Циклоидальные кривые

Циклоида – плоская кривая, которую описывает точка А, лежащая на окружности, которая

катится без скольжения по прямой CD (рис. 79 а).

Эпициклоида – плоская кривая, которую описывает точка А, лежащая на окружности, которая катится без скольжения, снаружи по направляющей окружности (рис. 79, б).

Гипоцоклоида – плоская кривая, которую описываетточка А, лежащая на окружности, ко­стится без скольжения внутри по направляющей окружности (рис. 79, в).

Построение циклоиды. На направляющей прямой ВС (рис. 79, а) откладывают длину произвольной окружности диаметра D, равную π D. Окружность диаметра D и отрезок АА ₁₂ ВС делят на равные части, например, на 12. Из точек делений ВС (1', 2', 3',..., 12') восставляют перпендикуляры до пересечения с продолжением горизонтальной оси окружности в точках О ₁, О ₂, …, О ₁₂, а из точек делений окружности (1, 2, 3, …, 12) проводят горизонтальные прямые. Из точек О ₁, О ₂, …, О ₁₂, как из центров, проводят окружности диаметра D, которые, пересекаясь с горизонтальными линиями, образуют точки А ₁, А₂, А₃, …, А ₁₂, принадлежащие циклоиде.

Построение эпициклоиды. Производящую окружность диаметра D и направляющую окружность радиуса R проводят так, чтобы они касались (рис. 79, б). Производящую окружность диаметра D делят на 12 равных частей. Из центра О ₀ радиусом, равным R + 0, 5D, проводят вспомогательную дугу.

Центральный угол α определяют по формуле

Разделив дугу направляющей окружности,

ограниченную углом α, на 12 равных частей, получают точки 1 ', 2', 3',..., 12'. Из центра О ₀ че­рез точки 1 ', 2 ', 3',..., 12' проводят прямые, которые продолжают до пересечения с вспомога­тельной дугой в точках О ₁, О ₂, О ₃, …, О ₁₂. Из центра О ₀ проводят вспомогательные дуги через точки делений 1...12 производящей окружности.

Из точек О ₁, О ₂, О ₃, …, О ₁₂, как из центров, проводят окружности диаметра D до пересечения с вспомогательными дугами в точках А₁, А₂, А ₃,..., А ₁₂, которые принадлежат эпициклоиде.

Построение гипоциклоиды аналогично построению эпициклоиды. Направляющую окружность радиуса R и производящую окружность диаметра D проводят так, чтобы они касались в точке А (рис. 79, в). Дугу направляющей окружности, ограниченную углом

делят на 12 равных частей; на столько же частей делят и производящую окружность. Точку деле­ния дуги направляющей окружности соединяют с точкой О ₀. В пересечении этих прямых с вспомогательной окружностью радиуса R = 0, 5 D получают точки О ₁, О ₂, О ₃, …, О ₁₂.

Из центра О ₀ через точки деления производя­щей окружности проводят вспомогательные дуги.

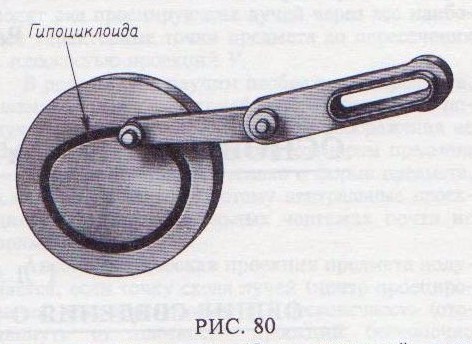
Из точек О ₁, О ₂, О ₃, …, О ₁₂ описывают окру­жности радиуса 0, 5D до пересечения с вспомогательными дугами в точках А₁, А₂, А ₃,..., А ₁₂, которые являются точками гипоциклоиды. Примером использования циклоидальных кривых в деталях может служить паз для пальца рычага (рис. 80). Он очерчен по гипоциклоиде.

ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ _________

1. Что такое сопряжение?

2. Какое сопряжение называется внешним, внутренним и смешанным?

3. Как определяются точки сопряжения?

4. По каким линиям рассекается конус плоскостями, различно расположенными относительно его оси?

5. Как построить спирали Архимеда?

6. Какая разница между циклоидой, эпициклоидой и гипоциклоидой?

7. Что называется уклоном и как определить его величину?

8. Что называется конусностью?

РАЗДЕЛ

II

ОСНОВЫ НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ