Кодирование микроопераций

Теперь рассмотрим, как можно использовать разряды поля микроопераций (МО). Различают [2] три способа кодирования поля микроопераций:

• горизонтальный;
• вертикальный;
• смешанный.

Ранее мы говорили, что управляющий автомат проектируется для выдачи в заданной последовательности наборов микроопераций из некоторого наперед определенного множества микроопераций Y = {y₁, y₂, …., y_n}

При горизонтальном способе кодирования каждой микрооперации y_i 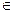{ y₁, …., y_n } ставится в соответствие разряд поля микроопераций микро­командного слова. В этом случае количество разрядов поля микроопераций N равно числу n различных микроопераций, вырабатываемых УА.

Достоинствами горизонтального способа кодирования являются:

• возможность формирования произвольных микрокоманд из заданного на­бора микроопераций;
• простота реализации схем формирования микроопераций, фактически — их отсутствие, т. к. выход каждого разряда поля микроопераций регистра микрокоманд является выходной линией УА — соответствующей микро­операцией.

Недостаток — чаще всего неэффективно используется память микрокоманд. Действительно, если число микроопераций УА составляет 80, а количество выполняемых в микрокоманде микроопераций — не более 6 (типичные ха­рактеристики для УА АЛУ), то в восьмидесятиразрядном поле микроопера­ций каждого микрокомандного слова будет не более 6 единиц.

При вертикальном способе кодирования в поле микроопераций помещается номер выполняемой микрооперации. При этом количество разрядов N, ко­торое следует предусмотреть в поле микроопераций, определяется выраже­нием: N=k 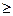log₂n. Достоинство способа в экономном использовании па­мяти микрокоманд. Недостаток— в невозможности реализовать в микро­команде более одной микрооперации.

Если реализуемые алгоритмы и структура ОА таковы, что в каждом такте дискретного времени выполняется не более одной микрооперации, то верти­кальный способ кодирования - оптимальное решение. В иных случаях мож­но попытаться преобразовать исходную микропрограмму к такому виду, что­бы в каждом такте выполнялось не более одной микрооперации. Например, если в микропрограмме (представленной в форме ГСА) имеется операторная вершина, в которой устанавливаются в исходное состояние несколько ячеек (элементов) памяти (и, следовательно, она включает несколько микроопера­ций), то ее можно заменить на несколько вершин, в каждой из которых уста­навливается только один элемент с помощью одной микрооперации. Теперь можно применить вертикальный способ кодирования, правда, при этом уве­личивается время реализации алгоритма.

Однако во многих случаях структура операционного автомата не допускает возможности разнесения во времени некоторых действий, управляемых раз­личными микрооперациями. Тогда вертикальный способ кодирования поля микроопераций не применим.

Вертикальный и горизонтальный способы кодирования — две крайности. Ис­тина обычно лежит " посередине". Рассмотрим смешанный способ кодирова­ния, идея которого состоит в следующем. Если во всех микропрограммах, реализуемых УА, нет микрокоманды с большим, чем s, числом микроопера­ций, то в поле микроопераций можно предусмотреть s подполей разряд­ностью k, в каждом из которых помещать номер нужной микрооперации. Такой способ позволяет в любой микрокоманде реализовать произвольную s-ку микроопераций, т. е. сохранить гибкость горизонтального кодирования, при возможном значительном сокращении разрядности поля микроопераций: N = s*k = s*log₂n. Так, для приведенного выше примера (n = 80, s = 6) оп­ределим k = 7 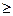log₂80, N = 7*6 = 42 (тоже, конечно, немало), что позволит почти вдвое сократить разрядность поля микроопераций по сравнению с гори­зонтальным способом кодирования.

Эффективность применения смешанного кодирования существенно зависит от значения s, которое может лежать в диапазоне 1 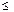s 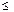n. При s = 1 имеем случай вертикального кодирования, при s = n — горизонтального.

Канонический способ смешанного кодирования, идея которого представлена выше, предполагает, что каждое из s подполей микроопераций содержит k разрядов, следовательно, в любом подполе можно закодировать любую микро­операцию у 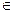Y. Возможно, например, построение микрокоманды, содержа­щей s одинаковых микроопераций y_i, y_i, …., y_i, что является явно бессмыс­ленным.

С целью сокращения разрядности полей микроопераций множество микро­операций Y разбивается на подмножества Y₁, Y₂, …, Y_p, такие, что

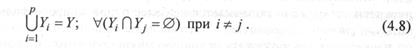
Каждое подполе поля микроопераций кодирует микрооперации только одного подмножества Y₁, Y. Поскольку |Y_i|< |Y|, разрядность k_i каждого из под-полей может быть меньше k. Очевидно, при " удачном" (пока скажем так) рас­пределении микроопераций по подмножествам можно будет реализовать любую операторную вершину ГСА микропрограммы с помощью одной микрокоманды (т. е. достигнуть быстродействия, характерного для горизон­тального способа кодирования), при этом значительно уменьшить разрядность поля микроопераций даже по сравнению с каноническим способом смешанно­го кодирования.

" Удачное" разбиение исходного множества микроопераций связано с поняти­ем совместимости (несовместимости) микроопераций [7]. Некоторые из используемых в микропрограмме микроопераций могут выполняться парал­лельно во времени, в то время как другие —• только последовательно. Свой­ство совокупности микроопераций, гарантирующее возможность их одно­временного выполнения, называется совместимостью. Микрооперации, не обладающие указанным свойством, называются несовместимыми.

Рассматриваются два аспекта совместимости. Совместимость, обусловленная содержанием операторов, реализуемых под действием микроопераций, назы­вается функциональной. Примером двух функционально несовместимых микроопераций могут служить следующая пара: (у₈: Счn: =0) и (у₁₅: Сч n: = n -1) и вообще любые микрооперации, присваивающие раз­личные значения одной и той же переменной.

Если невозможность одновременного выполнения микроопераций связана с ограничениями возможностей структуры операционного автомата, то такая несовместимость называется структурной. Например, операторы (Рг С: = Рг А) и (Рг D: = Рг B) функционально совместимы, но если в кон­кретной структуре ОА связь между этими регистрами осуществляется через общую магистраль (шину), то они структурно несовместимы.

Вернемся к способам разбиения исходного множества микроопераций на подмножества. Очевидно, в каждое подмножество следует включать только

взаимно несовместимые микрооперации. При проектировании УА возникает вопрос: какой тип совместимости микроопераций учитывать при разбиении исходного множества Y на подмножества?

Если несовместимыми считать только те микрооперации, которые принципи­ально нельзя реализовать на заданной (спроектированной) структуре ОА, то таких пар окажется немного, большинство микроопераций будут попарно совместимыми, следовательно, их необходимо включать в разные подмноже­ства. При этом число подмножеств р может превысить значение s и при­ближаться к n.

Если рассматривать в качестве совместимых только те микрооперации, кото­рые размещаются в одной операторной вершине реализуемых алгоритмов, а все остальные считать несовместимыми, даже если их можно выполнить од­новременно в структуре ОА (но не требуется при реализации данных алго­ритмов), то р® s, эффективность кодирования будет значительно выше. Правда, если потребуется модифицировать реализуемый алгоритм или доба­вить еще группу алгоритмов для реализации, и в одной операторной вершине окажутся микрооперации, включенные ранее в одно подмножество, придется заново перепроектировать УА.

Разработано несколько формальных методов [7] разбиения множества мик­роопераций на подмножества. В простейшем случае можно воспользоваться методом " прямого включения". Рассмотрим пример проектирования УАПЛ по заданной микропрограмме.