Пример проектирования УАЖЛ

Рассмотрим пример построения управляющего автомата Мура для устрой­ства, реализующего операцию деления. Операционный автомат (см. рис. 4.4) и ГСА микропрограммы (см. рис. 4.5) этого устройства были построены ранее.

Шаг 1. Выполним разметку микропрограммы. Для этого сопоставим каждой операторной вершине ГСА в произвольном порядке (например, слева напра­во и сверху вниз) символ состояния автомата из множества { a₂, a₃, …., a₁₄}. Начальную и конечную вершины сопоставим с начальным состоянием авто­мата a₁. Такая разметка показана на рис. 4.5.

Шаг 2. Построим граф автомата, заданного размеченной микропрограм­мой, которую получили на предыдущем шаге. Для этого вершины графа со­поставим с состояниями автомата a₂, a₃, …., a₁₄. Соединим ориентирован­ными ребрами те пары вершин графа, между которыми на ГСА микропро-

граммы существуют переходы, причем пометим ребра графа соответствую­щими условиями перехода. Если переход между двумя операторными вер­шинами микропрограммы осуществляется безусловно, то условие перехода на ребре графа — константа 1.

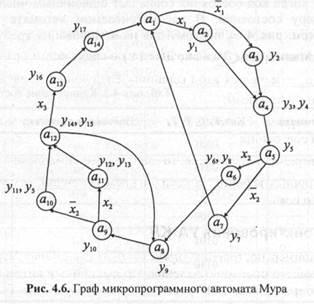
Построив таким образом граф, мы фактически задаем алфавиты внутренних состояний и входных символов и определяем функцию переходов. Для зада­ния алфавита выходных символов и функции выходов (для автомата Мура функция выходов зависит только от его состояний) следует сопоставить каж­дой вершине автомата в качестве выходного символа содержимое соответст­вующей операторной вершины ГСА микропрограммы. Таким образом, полу­чим граф микропрограммного автомата, который приведен на рис. 4.6.

Шаг 3. Кодирование алфавитов входных и выходных символов автомата дво­ичными кодами. Алфавит входных символов составляет множество двоичных переменных X = {x_l, х₂, x₃}, поэтому проблема кодирования входных симво­лов двоичными переменными здесь не стоит. Что касается кодирования сим­волов выходного алфавита, то отложим обсуждение этого вопроса до шага 8.

Шаг 4. В процессе кодирования внутренних состояний автомата могут ре­шаться проблемы исключения гонок в автомате, проблемы минимизации комбинационной схемы, обеспечивающей функцию переходов автомата. Для решения этих задач разработаны достаточно сложные алгоритмы, которые описаны в литературе, например, [2, 5]. Здесь мы не будем касаться этой сто­роны процедуры синтеза автомата.

Следует отметить, что проблемы гонок могут быть полностью решены при использовании в автомате двухтактных элементов памяти, причем способ кодирования состояний в этом случае роли не играет. Правда, затраты обору­дования при таком решении несколько возрастают, по сравнению с использо­ванием метода противогоночного кодирования, но во-первых, эффективность метода заметно проявится лишь при достаточно большом числе состояний автомата (25—40), а во-вторых, большинство современных интегральных элементов памяти (триггеров) выпускаются именно двухтактными. Примене­ние специальных методов кодирования " с учетом сложности комбинацион­ных схем" [2] так же обеспечивает заметный эффект лишь для достаточно громоздких автоматов.

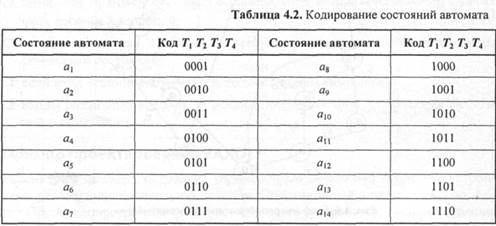
В нашем примере воспользуемся простейшим методом кодирования состоя­ний автомата, когда код состояния совпадает с двоичным числом, соответст­вующим номеру состояния. В рассматриваемом автомате насчитывается 14 состояний (см. рис. 4.6), поэтому для их кодирования требуется четырех­разрядный двоичный код (2⁴ > 14; 2³< 14) — табл. 4.2.

Шаг 5. Выбор элемента памяти (типа триггера). При выборе элемента памя­ти следует учитывать простоту управления им. С этой точки зрения удобнее выбирать триггеры, управляемые по единственному информационному вхо­ду — к таким относятся D- и Т-триггеры. В нашем примере в качестве эле­мента памяти автомата выберем синхронный двухтактный D-триггер. Оче­видно, для реализации нашего автомата понадобятся четыре D-триггера.

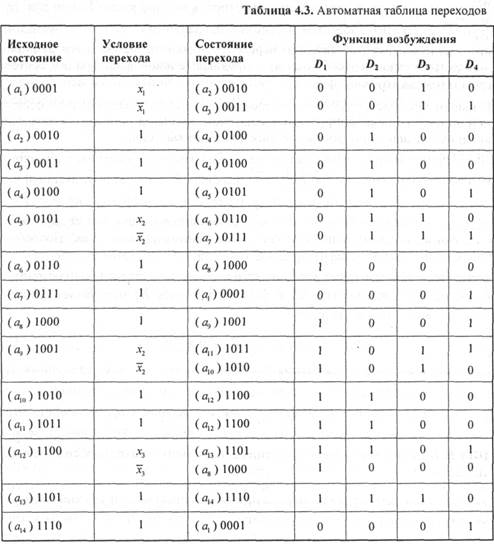
Шаг 6. Построение автоматной таблицы переходов (табл. 4.3).

Эта таблица практически описывает функцию переходов автомата, стро­ится по графу автомата и определяет, какие значения необходимо подать на управляющие входы триггеров на каждом переходе автомата в новое со­стояние. Строка таблицы соответствует одному переходу автомата. Таким образом, автоматная таблица содержит столько строк, сколько ребер в графе автомата (включая и петли, если они имеются в графе).

Шаг 7. Синтез комбинационной схемы, реализующей функцию переходов автомата. Эта комбинационная схема в нашем случае реализует четыре буле­вы функции D₁, D₂, D₃, D₄, зависящие от четырехразрядного двоичного кода состояния автомата Т₁Т₂Т₃Т₄ и трехбитного вектора входных символов x₁ x₂ x₃ Комбинационная схема, описываемая системой четырех булевых функций от семи переменных, должна обеспечивать переходы автомата в соответствии с графом рис. 4.6.

Для построения этой схемы можно построить четыре карты Карно для D₁, D₂, D₃, D₄, пo таблицам истинности, заданным соответствующими столбцами автоматной таблицы переходов, и минимизировать эти функции. Менее трудоемкий способ состоит в предварительной дешифрации состоя­ний автомата (булевы функции четырех переменных) и записи функций возбуждения через значения а_i и x_k. Воспользуемся последним способом, тем более, что дешифрированные состояния автомата пригодятся нам и на следующем шаге при формировании функции выходов.

Итак, предусмотрим дешифратор, на входы которого поступает двоичный код состояния автомата 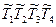, а на выходах формируется унитарный код 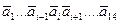. Кстати, поскольку на входах дешифратора не могут по­явиться комбинации 0000 и 1111 (их мы не использовали при кодировании состояний), то схему дешифратора можно минимизировать. (Как? Попробуй­те построить такой дешифратор самостоятельно.) Рассмотрим столбец D_l ав­томатной таблицы переходов, отметив те наборы входных переменных функции возбуждения (из {а} и {x}), на которых D_l принимает единич­ные значения. Можно записать:

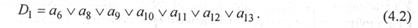
Обратите внимание, что функция D_l не зависит от входных переменных {х} (частный случай!). Действительно, переход, например, из состояния а₉ в за­висимости от значения х₂ может произойти в а₁₀ или в а₁₁, но в обоих этих состояниях значение старшего разряда кодов одинаково. То же для D_l можно сказать и обо всех остальных переходах, зависящих от входных символов a₁, a₅, …., a₁₂ Теперь запишем булевы выражения для остальных функций возбуж­дения.

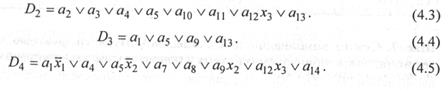
Шаг 8. Синтез комбинационной схемы, реализующей функцию выходов. Функция выходов автомата Мура зависит только от его внутреннего состоя­ния и задана непосредственно на графе автомата (см. рис. 4.6). Выходами микропрограммного автомата являются микрооперации, поступающие в точки управления операционного автомата. Поэтому выходные символы микропрограммного автомата обычно не кодируют, а формируют на выходе значение вектора микроопераций. При большом числе микроопераций с целью уменьшения связности между ОА и УА на вход ОА передают не век­тор микроопераций, а номер активной в данном такте микрооперации. Под­робнее об этом — в следующем разделе.

Из графа автомата (см. рис. 4.6) видно, что микрооперация у₁ должна вырабатываться автоматом, когда он находится в состоянии а₂, микроопе­рация y₂ — в состоянии a₃ и т.д. Микрооперация у₅ должна вырабаты­ваться автоматом, находящимся в состоянии а₅ и а₁₀. Запишем функцию выходов автомата в виде системы булевых функций (Напомним, что переменные а₁, а₂,..., а₁₄ являются булевыми, принимающими единичное значение, когда автомат находится в соответствующем состоянии, и нулевое значение — во всех остальных случаях)

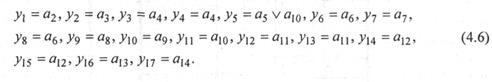
Шаг 9. Теперь изобразим функциональную схему управляющего автомата, используя выражения (4.2)—(4.6) с учетом выбранного типа элемента па­мяти.

Управляющий микропрограммный автомат с жесткой логикой (автомат Му­ра), изображенный на рис. 4.7, имеет три двоичных входа x_l, х₂, х₃, вход тактового сигнала CLK и семнадцать двоичных выходов — микрооперации y_l, y₂, …..., y_17.

Память автомата представлена четырьмя двухтактными синхронными D-триггерами, объединенными общей цепью синхронизации (CLK). Выходы триг­геров поступают на вход дешифратора DC " 4 à 16", на выходах которого формируется унитарный код текущего состояния автомата. Поскольку проек­тируемый автомат является автоматом Мура, выходы дешифратора фактиче­ски являются выходами управляющего автомата (значениями микроопера­ций). Исключение составляет микрооперация у₅, которая формируется как

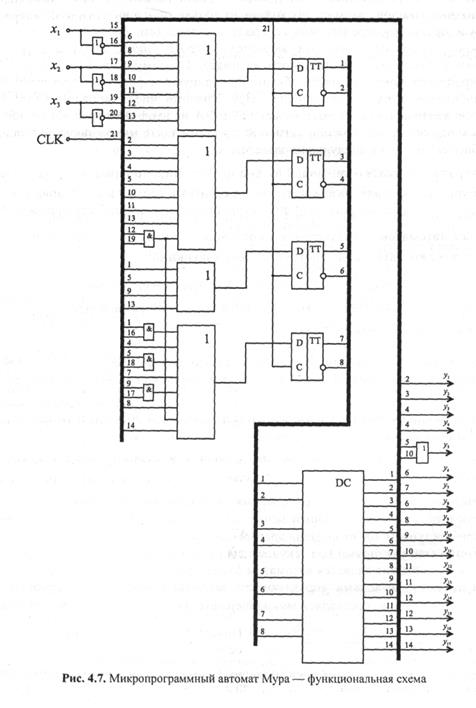дизъюнкция двух различных состоянии автомата, поскольку эта микроопера­ция присутствует в двух различных операторных вершинах исходной микро­программы (см. рис. 4.5).

Функции возбуждения триггеров формируют значения D_i, i 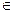{l, 2, 3, 4} на выходах одно- или двухуровневых схем, построенных согласно выражениям (4.2)—(4.5). Обратите внимание, что в выражениях (4.3) и (4.5) имеется одинаковый терм — a_l2х_3. На функциональной схеме выход конъюнктора, реализующего этот терм, поступает на два входа различных дизъюнкторов, " обеспечивая" одновременно две функции возбуждения — D₂ и D₄.

Схемы, реализующие функции возбуждения, можно построить иначе. Для примера рассмотрим выражение (4.4). Состояния автомата, входящие в это выражение, если выразить их через значения состояний триггеров, окажутся соседними и склеиваются. Действительно:

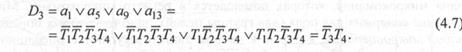
Очевидно, схема, реализованная по выражению (4. 7), будет проще, чем схема (4.4). Проверьте, можно ли подобным образом минимизировать выражения остальных функций возбуждения.

Итак, мы построили микропрограммный автомат с " жесткой" логикой. Да­вайте представим, что нам понадобилось незначительно изменить исходную микропрограмму, например, добавить еще одну операторную вершину. Прак­тически это приведет к необходимости полного перепроектирования всей схемы автомата. Это особенность автоматов с " жесткой" логикой является их серьезным недостатком.

Для того чтобы уменьшить зависимость структуры автомата от реализуемых им микропрограмм, используют управляющие автоматы с программируемой логикой.