Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Представление(кодирование) чисел

Билеты №3

Дискретное представление информации: двоичные числа; двоичное кодирование текста в памяти компьютера. Информационный объем текста.

Вся информация, которую обрабатывает компьютер должна быть представлена двоичным кодом с помощью двух цифр 0 и 1. Эти два символа принято называть двоичными цифрами или битами. С помощью двух цифр 0 и 1 можно закодировать любое сообщение. Это явилось причиной того, что в компьютере обязательно должно быть организованно два важных процесса: кодирование и декодирование.

Кодирование – преобразование входной информации в форму, воспринимаемую компьютером, т.е. двоичный код.

Декодирование – преобразование данных из двоичного кода в форму, понятную человеку.

С точки зрения технической реализации использование двоичной системы счисления для кодирования информации оказалось намного более простым, чем применение других способов. Действительно, удобно кодировать информацию в виде последовательности нулей и единиц, если представить эти значения как два возможных устойчивых состояния электронного элемента:

0 – отсутствие электрического сигнала;

1 – наличие электрического сигнала.

Эти состояния легко различать. Недостаток двоичного кодирования – длинные коды. Но в технике легче иметь дело с большим количеством простых элементов, чем с небольшим числом сложных.

Вам приходится постоянно сталкиваться с устройством, которое может находится только в двух устойчивых состояниях: включено/выключено. Конечно же, это хорошо знакомый всем выключатель. А вот придумать выключатель, который мог бы устойчиво и быстро переключаться в любое из 10 состояний, оказалось невозможным. В результате после ряда неудачных попыток разработчики пришли к выводу о невозможности построения компьютера на основе десятичной системы счисления. И в основу представления чисел в компьютере была положена именно двоичная система счисления.

Способы кодирования и декодирования информации в компьютере, в первую очередь, зависит от вида информации, а именно, что должно кодироваться: числа, текст, графические изображения или звук.

Представление(кодирование) чисел

Для записи информации о количестве объектов используются числа. Числа записываются с помощью набора специальных символов.

Система счисления — способ записи чисел с помощью набора специальных знаков, называемых цифрами.

Системы счисления подразделяются на позиционные и непозиционные.

В позиционных системах счисления величина, обозначаемая цифрой в записи числа, зависит от её положения в числе (позиции).

В непозиционных системах счисления величина, которую обозначает цифра, не зависит от положения в числе.

Непозиционные системы счисления.

Каноническим примером фактически непозиционной системы счисления является римская, в которой в качестве цифр используются латинские буквы: I обозначает 1, V - 5, X - 10, L - 50, C - 100, D - 500, M -1000. Натуральные числа записываются при помощи повторения этих цифр. При этом, если большая цифра стоит перед меньшей, то они складываются (принцип сложения), если же меньшая — перед большей, то меньшая вычитается из большей (принцип вычитания). Последнее правило применяется только во избежание четырёхкратного повторения одной и той же цифры.

Например, II = 1 + 1 = 2, здесь символ I обозначает 1 независимо от места в числе.

Для правильной записи больших чисел римскими цифрами необходимо сначала записать число тысяч, затем сотен, затем десятков и, наконец, единиц.

Пример: число 1988. Одна тысяча M, девять сотен CM, восемьдесят LXXX, восемь VIII. Запишем их вместе: MCMLXXXVIII.

MCMXCVIII = 1000+(1000-100)+(100-10)+5+1+1+1 = 1998

Позиционные системы счисления.

В позиционных системах счисления величина, обозначаемая цифрой в записи числа, зависит от её положения в числе (позиции). Количество используемых цифр называется основанием системы счисления.

Самой первой такой системой, когда счетным " прибором" служили пальцы рук, была пятеричная.

Следующей после пятеричной возникла двенадцатеричная система счисления. Возникла она в древнем Шумере. Некоторые учёные полагают, что такая система возникала у них из подсчёта фаланг на руке большим пальцем. Широкое распространение получила двенадцатеричная система счисления в XIX веке.

Следующая позиционная система счисления была придумана еще в Древнем Вавилоне, причем вавилонская нумерация была шестидесятеричная, т.е. в ней использовалось шестьдесят цифр! В более позднее время использовалась арабами, а также древними и средневековыми астрономами. Шестидесятеричная система счисления, как считают исследователи, являет собой синтез уже вышеупомянутых пятеричной и двенадцатеричной систем.

В настоящее время наиболее распространены десятичная, двоичная, восьмеричная и шестнадцатеричная системы счисления. Двоичная, восьмеричная (в настоящее время вытесняется шестнадцатеричной) и шестнадцатеричная система часто используется в областях, связанных с цифровыми устройствами, программировании и вообще компьютерной документации. Современные компьютерные системы оперируют информацией представленной в цифровой форме. Числовые данные преобразуются в двоичную систему счисления.

Десятичная система счисления — позиционная система счисления по основанию 10. Предполагается, что основание 10 связано с количеством пальцев рук у человека. Наиболее распространённая система счисления в мире. Для записи чисел используются символы 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, называемые арабскими цифрами.

Двоичная система счисления — позиционная система счисления с основанием 2. Используются цифры 0 и 1. Двоичная система используется в цифровых устройствах, поскольку является наиболее простой и удовлетворяет требованиям:

· Чем меньше значений существует в системе, тем проще изготовить отдельные элементы.

· Чем меньше количество состояний у элемента, тем выше помехоустойчивость и тем быстрее он может работать.

· Простота создания таблиц сложения и умножения — основных действий над числами

При одновременной работе с несколькими системами счисления для их различения основание системы обычно указывается в виде нижнего индекса, который записывается в десятичной системе:

123₁₀ — это число 123 в десятичной системе счисления;

1111011₂ — то же число, но в двоичной системе.

Двоичное число 1111011 можно расписать в виде: 1111011₂ = 1*2⁶ + 1*2⁵ + 1*2⁴ + 1*2³ + 0*2² + 1*2¹ + 1*2⁰.

Двоичная система счисления обладает такими же свойствами, что и десятичная, только для представления чисел используются не 10 цифр, а всего две. Соответственно и разряд числа называют не десятичным, а двоичным.

Перевод из десятичной системы счисления в систему счисления с основанием p осуществляется последовательным делением десятичного числа и его десятичных частных на p, а затем выписыванием последнего частного и остатков в обратном порядке.

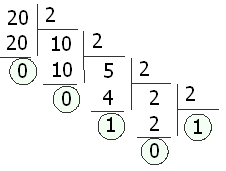
Переведем десятичное число 2010 в двоичную систем счисления (основание системы счисления p=2). В итоге получили 20₁₀ = 10100₂.

Двоичное кодирование текстовой информации

Начиная с 60-х годов, компьютеры все больше стали использовать для обработки текстовой информации и в настоящее время большая часть ПК в мире занято обработкой именно текстовой информации.

Традиционно для кодирования одного символа используется количество информации = 1 байту (1 байт = 8 битов).

Для кодирования одного символа требуется один байт информации.

Учитывая, что каждый бит принимает значение 1 или 0, получаем, что с помощью 1 байта можно закодировать 256 различных символов. (2⁸ = 256)

Кодирование заключается в том, что каждому символу ставится в соответствие уникальный двоичный код от 00000000 до 11111111 (или десятичный код от 0 до 255).

Важно, что присвоение символу конкретного кода – это вопрос соглашения, которое фиксируется кодовой таблицей.

Таблица, в которой всем символам компьютерного алфавита поставлены в соответствие порядковые номера (коды), называется таблицей кодировки.

Для разных типов ЭВМ используются различные кодировки. С распространением IBM PC международным стандартом стала таблица кодировки ASCII (A merican S tandard C ode for I nformation I nterchange) – Американский стандартный код для информационного обмена.

Стандартной в этой таблице является только первая половина, т.е. символы с номерами от 0 (00000000) до 127 (0111111). Сюда входят буква латинского алфавита, цифры, знаки препинания, скобки и некоторые другие символы.

Остальные 128 кодов используются в разных вариантах. В русских кодировках размещаются символы русского алфавита.

В настоящее время существует 5 разных кодовых таблиц для русских букв (КОИ8, СР1251, СР866, Mac, ISO).

В настоящее время получил широкое распространение новый международный стандарт Unicode, который отводит на каждый символ два байта. С его помощью можно закодировать 65536 (2¹⁶= 65536) различных символов.

Сегодня очень многие люди для подготовки писем, документов, статей, книг и пр. используют компьютерные текстовые редакторы. Компьютерные редакторы, в основном, работают с алфавитом размером 256 символов.

В этом случае легко подсчитать объем информации в тексте. Если 1 символ алфавита несет 1 байт информации, то надо просто сосчитать количество символов; полученное число даст информационный объем текста в байтах.

Пусть небольшая книжка, сделанная с помощью компьютера, содержит 150 страниц; на каждой странице — 40 строк, в каждой строке — 60 символов. Значит страница содержит 40x60=2400 байт информации. Объем всей информации в книге: 2400 х 150 = 360 000 байт.

Обратите внимание! Цифры кодируются по стандарту ASCII в двух случаях – при вводе-выводе и когда они встречаются в тексте. Если цифры участвуют в вычислениях, то осуществляется их преобразование в другой двоичных код.

Возьмем число 57.

При использовании в тексте каждая цифра будет представлена своим кодом в соответствии с таблицей ASCII. В двоичной системе это – 00110101 00110111.

При использовании в вычислениях, код этого числа будет получен по правилам перевода в двоичную систему и получим – 00111001.