
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Требования к оформлению отчета. 3 страница
|
|
53. Выборочный метод математической статистики. Выборочные характеристики. Эмпирическая функция распределения.
54. Критерий согласия хи-квадрат.
55. Линейный регрессионный анализ. Метод наименьших квадратов. Ранговая корреляция по Спирману. Подбор линеаризующего преобразования. Примеры постановок экономических задач, решаемых с помощью этого метода.
Тест
| № вопроса | Формулировка вопроса | Варианты ответа | Правильный ответ(ы) |
Игральная кость подбрасывается один раз. Рассматриваются следующие события:
 , ,
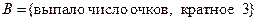 , ,
 , ,
 .
Отметьте среди перечисленных пары несовместных событий. .
Отметьте среди перечисленных пары несовместных событий.
| 1) B и D 2) A и C 3) B и C 4) A и B 5) C и D | 1) 2) | |
Монета подбрасывается до первого появления герба, но не более трёх раз. Рассматриваются следующие события:
 , ,
 , ,
 , ,
 .
Отметьте среди перечисленных пары несовместных событий. .
Отметьте среди перечисленных пары несовместных событий.
| 1) A и B 2) A и C 3) B и C 4) B и D 5) C и D | 1) 2) 3) | |
Монета подбрасывается два раза. Рассматриваются следующие события:
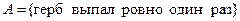 , ,
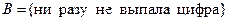 , ,
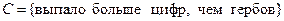 , ,
 .
Отметьте среди перечисленных пары несовместных событий. .
Отметьте среди перечисленных пары несовместных событий.
| 1) A и B 2) A и C 3) B и D 4) A и D 5) C и D | 1) 2) 3) | |
| Отметьте те из приведённых ниже соотношений над событиями, которые являются верными. | 1)  2)
2) 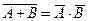 3)
3)  4)
4)  5)
5) 
| 1) 2) | |
| Отметьте те из приведённых ниже соотношений над событиями, которые являются верными. | 1)  2)
2) 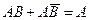 3)
3)  4)
4)  5)
5) 
| 1) 2) | |
| Отметьте те из приведённых ниже соотношений над событиями, которые являются верными. | 1)  2)
2)  3)
3) 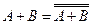 4)
4)  5)
5) 
| 1) 2) 3) | |
Известно, что A и B – наблюдаемые события в эксперименте, причём 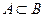 , ,  , ,  . Отметьте верные утверждения среди приведённых ниже. . Отметьте верные утверждения среди приведённых ниже.
| 1)  2)
2)  3)
3)  4)
4)  5)
5) 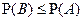 6)
6) 
| 1) 2) 3) | |
Известно, что A и B – наблюдаемые события в эксперименте, причём 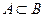 , , 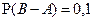 , ,  . Отметьте верные утверждения среди приведённых ниже. . Отметьте верные утверждения среди приведённых ниже.
| 1)  2)
2)  3)
3)  4)
4) 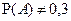 5)
5)  6)
6) 
| 1) 2) 3) | |
Известно, что A и B – наблюдаемые события в эксперименте, причём 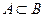 , , 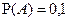 , ,  . Отметьте верные утверждения среди приведённых ниже. . Отметьте верные утверждения среди приведённых ниже.
| 1) 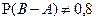 2)
2)  3)
3)  4)
4)  5)
5)  6)
6) 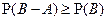
| 1) 2) 3) | |
Известно, что A и B – наблюдаемые события в эксперименте, причём 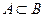 , ,  , , 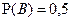 . Отметьте верные утверждения среди приведённых ниже. . Отметьте верные утверждения среди приведённых ниже.
| 1)  2)
2) 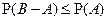 3)
3) 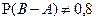 4)
4)  5)
5)  6)
6) 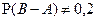
| 1) 2) 3) | |
| В урне лежат только 3 белых, 4 чёрных и 5 красных шаров. Какова вероятность вынуть из урны белый шар? | 1)  2)
2)  3)
3)  4)
4)  5) нет верного ответа среди предложенных вариантов
5) нет верного ответа среди предложенных вариантов
| 1) | |
| В урне лежат только 3 белых, 4 чёрных и 5 красных шаров. Какова вероятность вынуть из урны красный шар? | 1)  2)
2)  3)
3)  4)
4)  5) нет верного ответа среди предложенных вариантов
5) нет верного ответа среди предложенных вариантов
| 1) | |
| В урне лежат только 3 белых, 4 чёрных и 5 красных шаров. Какова вероятность вынуть из урны чёрный шар? | 1) 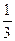 2)
2)  3)
3)  4)
4)  5) нет верного ответа среди предложенных вариантов
5) нет верного ответа среди предложенных вариантов
| 1) | |
| В урне лежат только 3 белых, 4 чёрных и 5 красных шаров. Какова вероятность вынуть из урны белый или красный шар? | 1)  2)
2)  3)
3) 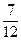 4)
4)  5) нет верного ответа среди предложенных вариантов
5) нет верного ответа среди предложенных вариантов
| 1) | |
| В урне лежат только 3 белых, 4 чёрных и 5 красных шаров. Какова вероятность вынуть из урны красный или чёрный шар? | 1)  2)
2)  3)
3) 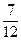 4)
4)  5) нет верного ответа среди предложенных вариантов
5) нет верного ответа среди предложенных вариантов
| 1) | |
| В урне лежат только 3 белых, 4 чёрных и 5 красных шаров. Какова вероятность вынуть из урны белый или чёрный шар? | 1) 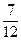 2)
2)  3)
3)  4)
4)  5) нет верного ответа среди предложенных вариантов
5) нет верного ответа среди предложенных вариантов
| 1) | |
| Сколько имеется перестановок цифр 0, 1, 2, …, 9 в которых цифра 1 следует непосредственно за цифрой 0? | 1)  2)
2)  3)
3)  4)
4)  5) нет верного ответа среди предложенных вариантов
5) нет верного ответа среди предложенных вариантов
| 1) | |
| На конференции должны выступить докладчики А, В, С, D и F, причём В не может выступать раньше А. Сколькими способами можно установить очерёдность выступлений? | 1)  2)
2)  3)
3)  4)
4)  5) нет верного ответа среди предложенных вариантов
5) нет верного ответа среди предложенных вариантов
| 1) | |
| У дедушки есть 8 различных конфет, которые он даёт своим 8 внукам, причём каждый внук получает только одну конфету. Сколькими способами это можно сделать? | 1)  2)
2)  3)
3) 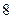 4)
4) 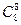 5) нет верного ответа среди предложенных вариантов
5) нет верного ответа среди предложенных вариантов
| 1) | |
| У мальчика имеется 8 разных почтовых марок. Сколькими способами он может подарить своему другу 4 марки из этой коллекции? | 1)  2)
2)  3)
3)  4)
4) 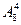 5) нет верного ответа среди предложенных вариантов
5) нет верного ответа среди предложенных вариантов
| 1) | |
| Сколькими способами 7 человек могут занять кресла в президиуме собрания, если организаторы собрания подготовили для этой цели 10 разных кресел? | 1)  2)
2) 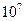 3)
3)  4)
4)  5) нет верного ответа среди предложенных вариантов
5) нет верного ответа среди предложенных вариантов
| 1) | |
| Сколько существует 7-значных чисел, в записи которых не содержится других цифр, кроме 2, 4, 6 и 8? | 1)  2)
2)  3)
3) 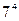 4)
4)  5) нет верного ответа среди предложенных вариантов
5) нет верного ответа среди предложенных вариантов
| 1) | |
| Каким числом способов можно купить 10 тетрадей, если в продаже имеются тетради 5 типов? | 1) нет верного ответа среди предложенных вариантов
2)  3)
3) 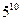 4)
4)  5)
5) 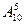
| 1) | |
| Имеются 3 экземпляра одной книги, 4 – другой и 8 – третьей. Каким числом способов эти книги можно вручить 15 детям, чтобы каждому досталось по одной книге? | 1)  2)
2)  3)
3)  4)
4)  5) нет верного ответа среди предложенных вариантов
5) нет верного ответа среди предложенных вариантов
| 1) | |
| Сколько новых «слов» можно составить, переставляя буквы в слове «БЕЛЛЕТРИСТИКА»? | 1)  2)
2)  3)
3)  4)
4)  5) нет верного ответа среди предложенных вариантов
5) нет верного ответа среди предложенных вариантов
| 1) | |
| У бабушки есть 5 различных фруктов, которые она даёт своим 8 внукам. Сколькими способами это можно сделать? | 1) 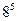 2)
2)  3)
3) 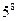 4)
4) 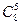 5) нет верного ответа среди предложенных вариантов
5) нет верного ответа среди предложенных вариантов
| 1) | |
| Сколькими способами можно разложить 20 одинаковых канцелярских скрепок по 3 разным коробкам? | 1) нет верного ответа среди предложенных вариантов
2)  3)
3) 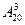 4)
4) 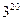 5)
5) 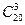
| 1) | |
| В конверте среди 100 фотографий находятся две разыскиваемые. Из конверта наудачу извлечено 10 фотографий. Найдите вероятность того, что среди них окажутся обе нужные. | 1)  2)
2)  3)
3) 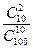 4)
4) 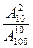 5) нет верного ответа среди предложенных вариантов
5) нет верного ответа среди предложенных вариантов
| 1) | |
| В ящике 100 одинаковых деталей, из них 10 бракованных. Наудачу извлечены 4 детали. Найдите вероятность того, что среди извлечённых деталей нет бракованных. | 1) 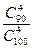 2)
2) 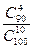 3)
3)  4)
4)  5) нет верного ответа среди предложенных вариантов
5) нет верного ответа среди предложенных вариантов
| 1) | |
| В ящике 100 одинаковых изделий, из них 5 окрашенных. Наудачу извлечены 3 изделия. Найдите вероятность того, что все извлечённые изделия окрашенные. | 1)  2)
2)  3)
3)  4)
4)  5) нет верного ответа среди предложенных вариантов
5) нет верного ответа среди предложенных вариантов
| 1) | |
| 2 студента МГАДА, 3 студента МАИ и 4 студента МГУ наугад рассаживаются в три вагона. Для каждого пассажира вероятность оказаться в любом из вагонов одинакова. Найдите вероятность того, что два студента МГАДА окажутся в разных вагонах. | 1) 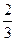 2)
2) 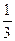 3)
3) 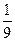 4)
4) 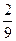 5) нет верного ответа среди предложенных вариантов
5) нет верного ответа среди предложенных вариантов
| 1) | |
| На отдельных карточках написаны 3 буквы А, 2 буквы Н и 1 буква С. Ребёнок берёт карточки в случайном порядке и прикладывает одну к другой. Какова вероятность того, что получится слово «АНАНАС»? | 1)  2)
2)  3)
3)  4)
4)  5) нет верного ответа среди предложенных вариантов
5) нет верного ответа среди предложенных вариантов
| 1) | |
| Из цифр 1, 2, 3 наугад составляется шестизначное число. Найдите вероятность того, что получится чётное число, содержащее всего одну цифру 2. | 1)  2)
2)  3)
3)  4)
4) 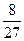 5) нет верного ответа среди предложенных вариантов
5) нет верного ответа среди предложенных вариантов
| 1) | |
| На плоскости начерчены две концентрические (с общим центром) окружности, радиусы которых равны 5 см и 10 см соответственно. Найдите процент испытаний, в которых точка, брошенная наудачу в большой круг, попадёт в кольцо, образованное построенными окружностями. | |||
| Быстро вращающийся диск разделён на чётное число секторов, окрашенных в белый и чёрный цвет (все секторы одинакового цвета равны между собой). Величина центрального угла в каждом секторе белого цвета в 3 раза больше величины центрального угла каждого сектора чёрного цвета. По диску произведён выстрел точечной пулей. Найдите процент выстрелов, в которых пуля попадёт в один из белых секторов. | |||
| На плоскость, разграфлённую параллельными прямыми, отстоящими, друг от друга на расстоянии 5 см, наудачу брошен круг радиусом 1 см. Найдите процент бросаний, в которых круг не пересечёт ни одной из прямых. | |||
| На плоскость с нанесённой на ней квадратной сеткой со стороной 5 см наудачу бросается монета диаметром 2 см. Найдите процент бросаний, в которых монета не пересечёт ни одной из прямых этой сетки. | |||
| В круг диаметром 8 см наудачу бросается точка. Найдите процент бросаний, в которых точка будет удалена от центра круга на расстояние, не превышающее половину радиуса этого круга. | |||
| На отрезок AB наудачу поставлена точка C. Затем на отрезке AC ставится ещё одна точка D. Какова вероятность того, что расстояние CD меньше половины длины отрезка AB? | 1) 0, 75 2) 0, 65 3) 0, 7 4) 0, 8 5) нет верного ответа среди предложенных вариантов | 1) | |
| На отрезок AB наудачу поставлена точка C. Затем на отрезке AC ставится ещё одна точка D. Какова вероятность того, что точка D ближе к точке B, чем к точке A? | 1) 0, 25 2) 0, 35 3) 0, 3 4) 0, 2 5) нет верного ответа среди предложенных вариантов | 1) | |
| На отрезке наудачу выбирают две точки. С какой вероятностью расстояние между ними будет меньше половины длины этого отрезка? | 1) 0, 75 2) 0, 65 3) 0, 8 4) 0, 7 5) нет верного ответа среди предложенных вариантов | 1) | |
| На отрезке AB наудачу выбирают точки C и D. С какой вероятностью точка C окажется ближе к D, чем к A? | 1) 0, 75 2) 0, 65 3) 0, 8 4) 0, 7 5) нет верного ответа среди предложенных вариантов | 1) | |
| На отрезок OA наудачу поставлены точки B и C (B левее C). Какова вероятность того, что длина отрезка BC будет меньше длины отрезка OB? | 1) нет верного ответа среди предложенных вариантов 2) 0, 2 3) 0, 25 4) 0, 75 5) 0, 8 | 1) | |
| На отрезок AB наудачу поставлена точка C. Затем на отрезке AC ставится ещё одна точка D. Какова вероятность того, что точка C ближе к точке D, чем к точке B? | 1) нет верного ответа среди предложенных вариантов 2) 0, 3 3) 0, 25 4) 0, 75 5) 0, 7 | 1) | |
Известно, что A и B – наблюдаемые события в эксперименте, причём  , ,  . Чему равна вероятность события . Чему равна вероятность события  ? ?
| 1) 0, 4 2) 0, 28 3) 0, 6 4) 0, 72 5) нет верного ответа среди предложенных вариантов | 1) | |
Известно, что A и B – наблюдаемые события в эксперименте, причём  , ,  . Чему равна вероятность события . Чему равна вероятность события  ? ?
| 1) 0, 5
2)  3) 0, 3
4) 0, 7
5) нет верного ответа среди предложенных вариантов
3) 0, 3
4) 0, 7
5) нет верного ответа среди предложенных вариантов
| 1) | |
Известно, что A и B – наблюдаемые события в эксперименте, причём  , , 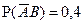 . Чему равна вероятность события . Чему равна вероятность события  ? ?
| 1) 0, 6 2) 0, 5 3) 0, 4 4) 0, 7 5) нет верного ответа среди предложенных вариантов | 1) | |
Известно, что A и B – наблюдаемые события в эксперименте, причём 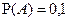 , , 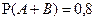 . Чему равна вероятность события . Чему равна вероятность события  ? ?
| 1) 0, 7 2) 0, 4 3) 0, 63 4) 0, 3 5) нет верного ответа среди предложенных вариантов | 1) | |
| В читальном зале имеется 5 учебников по теории вероятностей, из которых 3 в переплёте. Библиотекарь наудачу взял 2 учебника. Найдите процент случаев, в которых оба учебника окажутся в переплёте. | |||
| В читальном зале имеется 5 учебников по теории вероятностей, из которых 3 в переплёте. Библиотекарь наудачу взял 2 учебника. Найдите процент случаев, в которых оба учебника окажутся без переплёта. | |||
| В научной лаборатории работают 4 мужчины и 2 женщины. По табельным номерам наудачу отобрано 2 человека. Найдите процент случаев, в которых все отобранные лица окажутся мужчинами. | |||
| В научной лаборатории работают 3 мужчины и 3 женщины. По табельным номерам наудачу отобрано 2 человека. Найдите процент случаев, в которых все отобранные лица окажутся женщинами. | |||
| Из урны, содержащей 2 белых и 3 чёрных шара, наудачу и последовательно извлекают 2 шара без возвращения. Найдите процент случаев, в которых оба извлечённых шара окажутся белого цвета. | |||
| Из урны, содержащей 2 белых и 3 чёрных шара, наудачу и последовательно извлекают 2 шара без возвращения. Найдите процент случаев, в которых оба извлечённых шара окажутся чёрного цвета. | |||
Из колоды в 52 карты наугад вынимается одна карта. Рассматриваются следующие события:
 , ,
 , ,
 .
Отметьте верные ответы среди перечисленных. .
Отметьте верные ответы среди перечисленных.
| 1) события A и C независимы 2) события A и B независимы 3) события B и C независимы 4) любая пара событий зависима 5) любая пара событий независима | 1) 2) | |
Из колоды в 36 карт наугад вынимается одна карта. Рассматриваются следующие события:
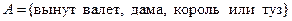 , ,
 , ,
 .
Отметьте верные ответы среди перечисленных. .
Отметьте верные ответы среди перечисленных.
| 1) события A и C независимы 2) события A и B независимы 3) события B и C независимы 4) любая пара событий зависима 5) любая пара событий независима | 1) 2) | |
Из колоды в 32 карты (без «шестёрок») наугад вынимается одна карта. Рассматриваются следующие события:
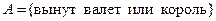 , ,
 , ,
 .
Отметьте верные ответы среди перечисленных. .
Отметьте верные ответы среди перечисленных.
| 1) события A и C независимы 2) события A и B независимы 3) события B и C независимы 4) любая пара событий зависима 5) любая пара событий независима | 1) 2) | |
| Для сигнализации об аварии установлены два независимо работающих сигнализатора. Вероятность того, что при аварии сигнализатор сработает, равна 0, 9 для первого сигнализатора и 0, 8 для второго. Найдите процент случаев, в которых при аварии сработает хотя бы один сигнализатор. | |||
| Для сигнализации об аварии установлены два независимо работающих сигнализатора. Вероятность того, что при аварии сигнализатор сработает, равна 0, 9 для первого сигнализатора и 0, 8 для второго. Найдите процент случаев, в которых при аварии сработает ровно один сигнализатор. | |||
| Два стрелка независимо друг от друга стреляют по одной мишени. Вероятность попадания в мишень при одном выстреле для первого стрелка равна 0, 8, для второго – 0, 7. Найдите процент случаев, в которых при одном залпе в мишень попадёт только один из стрелков. | |||
| Два стрелка независимо друг от друга стреляют по одной мишени. Вероятность попадания в мишень при одном выстреле для первого стрелка равна 0, 8, для второго – 0, 7. Найдите процент случаев, в которых при одном залпе в мишень попадёт хотя бы один из стрелков. | |||
| Студент разыскивает нужную ему формулу, заказав в читальном зале библиотеки два справочника. Вероятность того, что формула есть в первом справочнике, равна 0, 6, во втором – 0, 7. Найдите процент случаев, в которых нужная формула содержится только в одном справочнике. | |||
| Студент разыскивает нужную ему формулу, заказав в читальном зале библиотеки два справочника. Вероятность того, что формула есть в первом справочнике, равна 0, 6, во втором – 0, 7. Найдите процент случаев, в которых нужная формула содержится хотя бы в одном справочнике. | |||
| В ящике содержится 40 деталей, изготовленных на заводе №1, и 60 деталей, изготовленных на заводе №2. Вероятность того, что деталь, изготовленная на заводе №1, отличного качества, равна 0, 9. Для деталей, изготовленных на заводе №2, эта вероятность равна 0, 8. Найдите процент случаев, в которых наудачу взятая из ящика деталь окажется отличного качества. | |||
| Имеется 10 винтовок, 6 из которых снабжено оптическим прицелом. Вероятность того, что стрелок поразит мишень при выстреле из винтовки с оптическим прицелом, равна 0, 9; для винтовки без оптического прицела эта вероятность равна 0, 7. Найдите процент случаев, в которых стрелок поразит мишень, произведя один выстрел из наудачу взятой винтовки. | |||
| Число грузовых машин, проезжающих по шоссе, на котором стоит автозаправочная станция, относится к числу легковых машин, проезжающих по тому же шоссе, как 3: 2. Вероятность того, что будет заправляться грузовая машина, равна 0, 1; для легковой машины эта вероятность равна 0, 2. Найдите процент случаев, в которых проезжающая по шоссе машина подъедет к станции для заправки. | |||
| Спортсмены двух групп сдают квалификационные нормы. В первой группе 10 спортсменов, во второй – 15. Вероятности выполнения квалификационных норм спортсменом каждой группы соответственно равны 0, 8 и 0, 6. Найдите процент случаев, в которых наудачу выбранный из этих групп спортсмен выполнит квалификационную норму. | |||
| Экзамен на получение водительских прав пришли сдавать 20 человек, обучавшихся в городской автошколе, и 5 человек, окончивших заочные курсы по вождению автомобиля. Вероятность сдачи экзамена с первого раза для выпускников автошколы равна 0, 8, а для заочников – 0, 4. Найдите процент случаев, в которых наудачу выбранный из этих групп человек сдаст экзамен с первого раза. | |||
| После осмотра больного врач считает, что возможно одно из двух заболеваний C (гарантия 60%) или D (гарантия 40%). Для уточнения диагноза больного направляют на анализ, исход которого даёт положительную реакцию при заболевании C в 40% случаев, а при заболевании D – в 20% случаев. Анализ дал положительную реакцию. Найдите процент случаев, в которых у больного имеется заболевание C. | |||
| После осмотра больного врач считает, что возможно одно из двух заболеваний C (гарантия 60%) или D (гарантия 40%). Для уточнения диагноза больного направляют на анализ, исход которого даёт положительную реакцию при заболевании C в 40% случаев, а при заболевании D – в 20% случаев. Анализ дал положительную реакцию. Найдите процент случаев, в которых у больного имеется заболевание D. | |||
| Известно, что в среднем 20% выпускников школ способно обучаться в вузе. Упрощённая схема контроля признаёт выпускника способным к обучению в вузе с вероятностью 0, 8, если он действительно таковым является, и с вероятностью 0, 3, если он неспособен к обучению в вузе. Выбранный наудачу выпускник прошёл упрощённый контроль и был признан способным к обучению в вузе. Найдите процент случаев, в которых признанный способным к обучению в вузе выпускник действительно таковым является. | |||
| Известно, что в среднем 20% выпускников школ способно обучаться в вузе. Упрощённая схема контроля признаёт выпускника способным к обучению в вузе с вероятностью 0, 8, если он действительно таковым является, и с вероятностью 0, 3, если он неспособен к обучению в вузе. Выбранный наудачу выпускник прошёл упрощённый контроль и был признан способным к обучению в вузе. Найдите процент случаев, в которых признанный способным к обучению в вузе выпускник таковым не является. | |||
| На радиолокационную станцию (РЛС) в 80% случаев поступает только шум (нет цели), а в 20% случаев – смесь сигнала с шумом (есть цель). Известно, что решающее устройство РЛС при наличии только шума может ошибиться и зарегистрировать цель с вероятностью 0, 05; а при наличии сигнала с шумом цель правильно регистрируется с вероятностью 0, 8. Решающее устройство РЛС зарегистрировало цель. Найдите процент случаев, в которых РЛС не ошиблась? | |||
| На радиолокационную станцию (РЛС) в 80% случаев поступает только шум (нет цели), а в 20% случаев – смесь сигнала с шумом (есть цель). Известно, что решающее устройство РЛС при наличии только шума может ошибиться и зарегистрировать цель с вероятностью 0, 05; а при наличии сигнала с шумом цель правильно регистрируется с вероятностью 0, 8. Решающее устройство РЛС зарегистрировало цель. Найдите процент случаев, в которых РЛС ошиблась? |
|
|
