Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Тема 1.4. Механические колебания.

Основные понятия и термины по теме:

Механические колебания. Гармонические колебания. Амплитуда колебаний. Период. Частота. Фаза. Циклическая частота. Математический маятник. Пружинный маятник. Резонанс.

План изучения темы:

1. Механические колебания. Классификация колебаний.

2. Характеристики колебаний.

3. Резонанс.

Краткое изложение теоретических вопросов:

Механические колебания – движения тел или частей тел, характеризующиеся определённой повторяемостью во времени.

различают периодические и непериодические колебания.

Периодическими называют колебания, при которых координата и другие характеристики тела описываются периодическими функциями времени.

Колебания можно классифицировать:

Ι. По условиям их возникновения:

а) свободные (собственные) колебания – колебания, возникающие под действием внутренних сил, после выведения системы из положения равновесия.

б) вынужденные колебания – колебания, возникающие под действием внешних периодических сил.

Ι Ι. По характеру изменения во времени кинематических характеристик:

а) пилообразные и прямоугольные

б) затухающие и нарастающие

в) гармонические

Характеристиками колебаний являются:

1. Амплитуда колебаний А – наибольшее отклонение колеблющегося тела от положения равновесия.
2. Период колебания Т – время, через которое движение тела полностью повторяется, т.е. совершается одно полное колебание.
3. Частота колебаний ν – физическая величина, показывающая число колебаний, совершаемых за 1с.
4. Циклическая частота ω – это число колебаний, совершаемых за 2π секунд.
5. Фаза φ – называют аргумент функции, описывающей колебательный процесс.

Гармонические колебания – колебания, при которых физическая величина, характеризующая эти колебания, изменяются во времени по закону косинуса или синуса:

Математический маятник – это колеблющаяся материальная точка, подвешенная на невесомой и нерастяжимой нити.

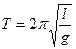, где

l- длина нити, g – ускорение свободного падения.

Пружинный маятник – это колеблющееся тело, прикреплённое к пружине.

, где

m – масса груза, k – коэффициент жёсткости пружины.

При вынужденных колебаниях может наблюдаться явление резкого возрастания амплитуды системы – резонанс. Это явления возникает тогда, когда частота вынуждающей силы приближается к собственной частоте колебаний этой системы.

Лабораторные работа «Изучение зависимости периода колебаний нитяного маятника от длины нити».

Цель работы: вычислить период колебания нитяного маятника, изучить зависимость периода колебаний нитяного маятника от длины нити.

Оборудование: шарик с отверстием, нить, штатив с муфтой и кольцом, часы с секундной стрелкой, линейка.

Ход работы:

Ι. Проверить справедливость формулы вычисления периода колебания математического маятника:

1. Установите на краю стола штатив. У его верхнего конца укрепите при помощи муфты кольцо и подвесьте к нему шарик на нити. Шарик должен висеть на расстоянии 3-5 см от пола.

2. Отклоните маятник от положения равновесия на 5-8 см и отпустите его.

3. Измерьте длину подвеса мерной лентой или линейкой.

4. Измерьте время Δ t, за которое маятник выполняет 20 полных колебаний (N).

5. Повторите измерения Δ t (не изменяя условий опыта) и найдите среднее значение Δ t_ср.

6. Вычислите среднее значение периода колебаний Т_ср по среднему значению Δ t_ср:

Т_ср=Δ t_ср/N (1)

7. Полученные результаты запишите в таблицу:

8. Вычислите период колебания нитяного маятника по формуле:

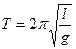(2)

9. Сравните полученные результаты, сделайте вывод.

Ι Ι. Изучить зависимость периода колебания нитяного маятника от длины нити.

1. Возьмите подвес нитяного маятника длиной 15см.

2. Отклоните маятник от положения равновесия на 5-8 см и отпустите его.

3. Измерьте время Δ t, за которое маятник совершает 20 полных колебаний (N).

4. Вычислите по формуле (1) период колебания, запишите в таблицу.

5. Повторите опыт, изменив длину подвеса (30см, 45см), полученные результаты периодов запишите в таблицу.

6. Сравните периоды колебаний маятника Т₁, Т₂, Т₃.

7. Запишите вывод.

Практические занятия: