
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Решение 1. Таблица1 У1 Х1 (Х1–Х3)×tg αТ1-Р (Х1–Х3)×tg αТ3-Р У2
|
|
Исходные данные:
Координаты пунктов Т1, Т2, Т3;
Измеренные углы β 1, β 2
Таблица1
| У1 | Х1 | (Х1–Х3)× tg α Т1-Р | (Х1–Х3)× tg α Т3-Р | ||||
| У2 | Х2 | (У1 –У3) | (У1 –У3) | ||||
| У3 | Х3 | ||||||
| У2 – У1 | Х2 – Х1 | А | В | ||||
| У3 – У2 | Х3 – Х2 | ХP – Х3 | ХP – Х1 | ||||
| У1 – У3 | Х1 – Х3 | Х3 | Х1 | ||||
| контроль | ХP | ХP | |||||
| β 1 | β 2 | (ХP–Х3)× tg α Т3-Р | (ХP–Х1)× tg α Т1-Р | ||||
| сtg β 1 | сtg β 2 | У3 | У1 | ||||
| (У2-У1)× сtg β 1 | (Х2–Х1)× сtg β 1 | УР | УР | ||||
| (У1–У3)× сtg β 2 | (Х1–Х3)× сtg β 2 | Контроль | |||||
| (Х3 – Х2) | (У3–У2) | У2 – УР | Окончательные значения | ||||
| Х2 – ХP | |||||||
| tg α T1-P | α Р-Т1 | tg α Р-Т2 | α Р-Т1 | ||||
| tg α T3-P | α Р-Т2 | α Р-Т2 | α Р-Т2 | ||||
| К | α Р-Т3 | α Р-Т3 |
Определение координат пункта Р из решения обратной засечки
(с использованием формулы Деламбра)
Решение 2 (1-ый вариант)
Исходные данные:
Координаты пунктов Т1, Т2, Т4;
Измеренные углы β 1, β 3
Таблица 2
| У1 | Х1 | (Х1–Х4)× tg α Т1-Р | (Х1–Х4)× tg α Т4 -Р | ||||
| У2 | Х2 | (У1 –У4) | (У1 –У4) | ||||
| У4 | Х4 | ||||||
| У2 - У1 | Х2 – Х1 | А | В | ||||
| У4 – У2 | Х4 – Х2 | ХP – Х4 | ХP – Х1 | ||||
| У1 – У4 | Х1 – Х4 | Х4 | Х1 | ||||
| контроль | ХP | ХP | |||||
| β 1 | β 3 | (ХP–Х4)× tg α Т4-Р | (ХP–Х1)× tg α Т1-Р | ||||
| сtg β 1 | сtg β 3 | У4 | У1 | ||||
| (У2 - У1)× сtg β 1 | (Х2–Х1)× сtg β 1 | УР | УР | ||||
| (У1 - У4)× сtg β 3 | (Х1–Х4)× сtg β 3 | Контроль | |||||
| (Х4 – Х2) | (У4–У2) | У2 - УР | Окончательные значения | ||||
| Х2 – ХP | |||||||
| tg α T1-P | α Р-Т1 | tg α Р-Т2 | α Р-Т1 | ||||
| tg α T4-P | α Р-Т2 | α Р-Т2 | α Р-Т2 | ||||
| К | α Р-Т4 | α Р-Т4 |
Определение координат пункта Р из решения обратной засечки
(с использованием формулы Деламбра)
Решение 2 (2-ой вариант)
Исходные данные:
Координаты пунктов Т1, Т3, Т4;
Измеренные углы β 2, β 3
Таблица 3
| У1 | Х1 | (Х1–Х4)× tg α Т1-Р | (Х1–Х4)× tg α Т4-Р | ||||
| У3 | Х3 | (У1 –У4) | (У1 –У4) | ||||
| У4 | Х4 | ||||||
| У3 - У1 | Х3 – Х1 | А | В | ||||
| У4 – У3 | Х4 – Х3 | ХP – Х4 | ХP – Х1 | ||||
| У1 – У4 | Х1 – Х4 | Х4 | Х1 | ||||
| контроль | ХP | ХP | |||||
| β 2 | β 3 | (ХP–Х4)× tg α Т4-Р | (ХP–Х1)× tg α Т1-Р | ||||
| сtg β 2 | сtg β 3 | У4 | У1 | ||||
| (У3-У1)× сtg β 2 | (Х3–Х1)× сtg β 2 | УР | УР | ||||
| (У1–У4)× сtg β 3 | (Х1–Х4)× сtg β 3 | Контроль | |||||
| (Х4 – Х3) | (У4–У3) | У3 - УР | Окончательные значения | ||||
| Х3– ХP | |||||||
| tg α T1-P | α Р-Т1 | tg α Р-Т3 | α Р-Т1 | ||||
| tg α T4-P | α Р-Т3 | α Р-Т3 | α Р-Т3 | ||||
| К | α Р-Т4 | α Р-Т4 |
Второе решение (2-ой вариант)
1. Вычисляют дирекционный угол начального направления (с твердого пункта Т1 на определяемый Р) по формуле Деламбра:

гдеХ1, У1; Х3, У3; Х4, У4 - координаты соответственно пунктов Т1, Т3, Т4;
β 2, β 3 – углы, измеренные от начального направления соответственно до третьего и четвертого направлений.
Значение дирекционного угла определяют по знаку tg α Т1-Р.
2. Выполняют контроль вычислений.
(Х3 – Х1) + (Х4 – Х3) + (Х1- Х4) = 0
(У3 – У1) + (У4 – У3) + (У1- У4) = 0
3. Вычисляют дирекционные углы 3-го и 4-го направлений (α Р-Т3, α Р-Т4) от пункта Р на твердые по ниже приведенным формулам, для этого сначала переходят от дирекционного угла α Т1-Р к его обратному значению.
α Р-Т1 = α Т1-Р ± 180о;
α Р-Т3 = α Р-Т1 + β 2 ;
α Р-Т4 = α Р-Т1 + β 3,
где α Т1-Р - дирекционный угол начального направления;
β 2, β 3 - измеренные углы от начального направления.
4. Вычисляют дважды координаты пункта Р по формулам Гаусса. По ним определяют координаты искомого пункта прямой угловой засечкой. В этих расчетных формулах используют дирекционные углы направлений с твердых пунктов на искомую точку, поэтому необходимо от ранее вычисленных направлений от искомого пункта на твердые пункты перейти к направлениям от твердых пунктов на определяемый пункт.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
α Т1-Р = α Р-Т1 ± 180о;
α Т3-Р = α Р-Т3 ± 180о;
α Т4-Р = α Р-Т4 ± 180о.


УР = У4 + (ХР – Х4)× tg α Т4-Р;
УР = У1+ (ХР - Х1)× tg α Т1-Р.
5. Для контроля правильности вычислений определяют дирекционный угол третьего направления, используя для этого координаты исходного пункта Т3 и вычисленные координаты пункта Р:
 .
.
Расхождение между вычисленными дирекционными углами разными способами не должно превышать 1''.
Примеры расчета координат пункта по формуле Деламбра приведены в таблицах 4, 5 и 6 соответственно – 1-ое, 2-ое (1-ый вариант) и 2-ое (2-ой вариант) решения.
На рис. 3 даны ориентированные схемы засечек для 31варианта, который дан в качестве примера определения координат пункта Р.
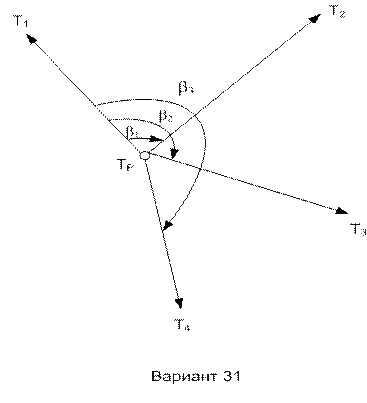
Рис. 3. Ориентированная схема засечки
Определение координат пункта Р из решения обратной засечки
(с использованием формулы Деламбра)
|
|
