
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Туннельный эффект.
|
|
При движении в потенциальном поле 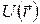 на любую частицу действует сила
на любую частицу действует сила
 . (3.1.1)
. (3.1.1)
В результате частица движется быстрее (если имеется потенциальная яма), или медленнее (если частица налетает на потенциальный барьер). Соответственно кинетическая энергия частицы возрастает или убывает. Потенциальный барьер может оказаться непреодолимой преградой для классической частицы, если высота барьера больше кинетической энергии частицы. Тогда точки, в которых высота барьера сравнивается с заданной кинетической энергией 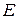 ,
,
 , (3.1.2)
, (3.1.2)
оказываются точками поворота. В этих точках сила (1) останавливает частицу, и она начинает двигаться в обратном направлении.
Область пространства, в которой  называется классически недоступной. Частица не может там находиться, поскольку значение кинетической энергии частицы должно было бы быть отрицательным, а импульс или скорость – мнимыми.
называется классически недоступной. Частица не может там находиться, поскольку значение кинетической энергии частицы должно было бы быть отрицательным, а импульс или скорость – мнимыми.
В квантовой физике, когда описание движения имеет вероятностный характер, поведение частицы в области барьера имеет иной характер. Рассмотрим поведение квантовой частицы в потенциальном поле сначала формально, а затем укажем стандартную квантовомеханическую интерпретацию полученных результатов.
Основные результаты квантовомеханического рассмотрения можно получить, изучая движение микрочастицы в одномерном потенциальном поле прямоугольной формы:
 (3.1.3)
(3.1.3)
Поскольку частица испытывает только стационарное воздействие (3), то ее энергия
имеет определенное значение, и описание движения частицы нужно проводить на основе стационарного уравнения Шредингера,
 , (3.1.4)
, (3.1.4)
где 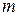 – масса частицы, а
– масса частицы, а 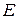 – ее полная энергия.
– ее полная энергия.
В соответствие с (3) решение уравнения (4) следует рассматривать в трех указанных в (3) областях. Тогда вместо (3) будем иметь
 ,
,
 , (3.1.5)
, (3.1.5)
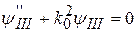 ,
,
где
 . (3.1.6)
. (3.1.6)
Обратим внимание на то, что при  (когда возникает туннельный эффект) волновое число частицы k чисто мнимая величина.
(когда возникает туннельный эффект) волновое число частицы k чисто мнимая величина.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
Общие решения уравнений Шредингера (6) имеют вид
 ,
,
 , (3.1.7)
, (3.1.7)
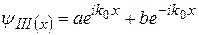 .
.
Решения (7) содержат шесть постоянных интегрирования. Их определяют из условий сшивки волновых функций и их производных на границах потенциального барьера:
 ,
,  при
при  . (3.1.8)
. (3.1.8)
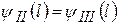 ,
,  при
при  . (3.1.9)
. (3.1.9)
Уравнения (8), (9) дают четыре алгебраических соотношения между постоянными интегрирования. Пятое уравнение появляется из физических соображений: мы рассматриваем падение частицы на барьер слева. Справа частицы на барьер не падают, поэтому коэффициент  . Остается неопределенным еще один коэффициент. Им можно считать величину А. Для определения А используется условие нормировки полной (сшитой) волновой функции,
. Остается неопределенным еще один коэффициент. Им можно считать величину А. Для определения А используется условие нормировки полной (сшитой) волновой функции,
 , (3.1.10)
, (3.1.10)
где интегрирование проводится по всем значениям  .
.
Решение четырех имеющихся уравнений определяет постоянные  . Их легко найти, но они имеют громоздкий вид. Поэтому мы не будем записывать все коэффициенты в явной форме. Например, важный для описания туннелирования коэффициент а равен
. Их легко найти, но они имеют громоздкий вид. Поэтому мы не будем записывать все коэффициенты в явной форме. Например, важный для описания туннелирования коэффициент а равен
 , (3.1.11)
, (3.1.11)
где
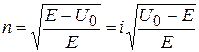 – (3.1.12)
– (3.1.12)
как и величина  , – является чисто мнимой.
, – является чисто мнимой.
По определению, отношение
 (3.1.13)
(3.1.13)
называется прозрачностью или коэффициентом прозрачности барьера при энергии падающей частицы Е.
Формулу (13) обычно несколько упрощают, записывая ее в виде
 . (3.1.14)
. (3.1.14)
Введение предэкспоненты  , слабо зависящей от параметров потенциального барьера, дает возможность выделить основные зависимости туннельного эффекта и применить формулы типа (14) к барьерам более сложной формы.
, слабо зависящей от параметров потенциального барьера, дает возможность выделить основные зависимости туннельного эффекта и применить формулы типа (14) к барьерам более сложной формы.
Отношение, аналогичное отношению (13),
 (3.1.15)
(3.1.15)
называется коэффициентом отражения частицы с энергией Е от барьера.
Интересно поведение частиц при  (надбарьерное прохождение). В отличие от классических частиц, которые проходят над барьером в первоначальном направлении движения (но с меньшей скоростью), квантовые частицы имеют вероятность отразиться от барьера и полететь в обратном направлении.
(надбарьерное прохождение). В отличие от классических частиц, которые проходят над барьером в первоначальном направлении движения (но с меньшей скоростью), квантовые частицы имеют вероятность отразиться от барьера и полететь в обратном направлении.
2. Туннельные диоды. Автоэлектронная эмиссия. Пробой Зинера.
Подстановка численных параметров в формулу (14) показывает, что электроны, например, с энергиями в десяток электрон-вольт с вероятностью порядка 10% проходят потенциальные барьеры толщиной в 1 ангстрем. Такие барьеры легко создать в структурах типа p – n переходов (так называемые туннельные диоды), используемых полупроводниковых микросхемах и в ряде измерительных приборов. Туннельные диоды имеют разную структуру. Один из наиболее распространенных типов создан на основе структуры полупроводник – тонкий слой диэлектрика – полупроводник или металл – диэлектрик – полупроводник. Туннельный эффект используется в полевых транзисторах, составляющих основу устройств флэш-памяти. Потенциальные барьеры при этом близки по своей форме к барьеру (1.3).
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.
Для новых пользователей первый месяц бесплатно. Зарегистрироваться в сервисе
Мы достаточно подобно обсудили туннельный эффект при наличии реального потенциального барьера, занимающего выделенную область пространства. Например, область  , как в случае (1.3). Туннельный эффект имеет место при автоэлектронной эмиссии. Так, при описании простейшей картины автоэлектронной эмиссии изучается треугольный барьер, сформированный постоянным электрическим полем вблизи поверхности металла:
, как в случае (1.3). Туннельный эффект имеет место при автоэлектронной эмиссии. Так, при описании простейшей картины автоэлектронной эмиссии изучается треугольный барьер, сформированный постоянным электрическим полем вблизи поверхности металла:
 . (3.2.1)
. (3.2.1)
Верхняя строчка в (1) относится к внутренней области металла, нижняя – к вакууму вне металла, где существует электрическое поле с напряженностью E. Разумеется, поле E не простирается до бесконечности, а «заканчивается» на электроде, создающем это поле (разность потенциалов или напряжение, приложенное к металлу, равно  ,
, 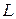 – расстояние между поверхностью металла и электродом.
– расстояние между поверхностью металла и электродом.
Изучение туннельного эффекта в потенциале (1) проводится с помощью уравнения Шредингера, в котором выделены две пространственные области, и имеются два сшиваемых решения. Как и в случае прямоугольного барьера, электроны имеют вероятность туннельным образом преодолеть барьер (1) и вылететь из металла в вакуум, что и составляет суть эффекта автоэлектронной эмиссии. Заметим, что автоэлектронная эмиссия – туннельный эффект, и этим отличается от внешнего фотоэффекта, в котором электрон проходит над барьером после поглощения энергии фотона.
Средний по энергиям электронов коэффициент прозрачности барьера при автоэлектронной эмиссии определяется формулой
 , (3.2.2)
, (3.2.2)
где  и
и  – постоянные, зависящие от типа металла, а
– постоянные, зависящие от типа металла, а 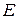 – напряженность поля. Очень интересно, что напряженность поля входит в знаменатель экспоненты. С точки зрения теории это означает, что туннельный эффект и автоэлектронная эмиссия не могут быть изучены в рамках теории возмущений.
– напряженность поля. Очень интересно, что напряженность поля входит в знаменатель экспоненты. С точки зрения теории это означает, что туннельный эффект и автоэлектронная эмиссия не могут быть изучены в рамках теории возмущений.
Умножая (2) на плотность потока электронов, падающего на поверхность (изнутри металла) получим плотность тока автоэлектронной эмиссии,
 . (3.2.3)
. (3.2.3)
Формула (3) достаточно хорошо подтверждается экспериментами.
Обратим внимание на то, что прозрачность и ток при автоэлектронной эмиссии выражены величинами «в среднем» и, как кажется, не содержат величину барьера  . Дело в том, что прозрачность треугольного барьера сильно зависит от энергии падающих на барьер электронов, что требует проведение усреднения. Кроме того, в реальных экспериментах потенциальный барьер (1) заметно деформируется. Деформация особенно сильна при автоэлектронной эмиссии из полупроводника. К деформации барьера приводят, по крайней мере, три причины. Во-первых, надо учитывать образование поверхностного заряда, являющегося источником внешнего поля (отрицательный поверхностный заряд деформирует барьер (1), делая его сглаженным или округлым). Во-вторых, приходится учитывать притяжение вылетевшего из металла электрона к оставшейся вместо него положительной дырке, что тоже оказывает заметное влияние на ток автоэлектронной эмиссии. Наконец, картина значительно усложняется наличием поверхностных энергетических уровней (уровни, существование которых предсказал И.Е. Тамм, так называемые таммовские уровни), которые образуются из-за обрыва на поверхности кристаллических цепочек.
. Дело в том, что прозрачность треугольного барьера сильно зависит от энергии падающих на барьер электронов, что требует проведение усреднения. Кроме того, в реальных экспериментах потенциальный барьер (1) заметно деформируется. Деформация особенно сильна при автоэлектронной эмиссии из полупроводника. К деформации барьера приводят, по крайней мере, три причины. Во-первых, надо учитывать образование поверхностного заряда, являющегося источником внешнего поля (отрицательный поверхностный заряд деформирует барьер (1), делая его сглаженным или округлым). Во-вторых, приходится учитывать притяжение вылетевшего из металла электрона к оставшейся вместо него положительной дырке, что тоже оказывает заметное влияние на ток автоэлектронной эмиссии. Наконец, картина значительно усложняется наличием поверхностных энергетических уровней (уровни, существование которых предсказал И.Е. Тамм, так называемые таммовские уровни), которые образуются из-за обрыва на поверхности кристаллических цепочек.
Большое влияние на величину и характер туннельного тока оказывает состояние поверхности и наличие на ней различных примесей.
Заметим также, что некоторые радиоактивные элементы распадаются, испуская 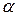 - частицы. Впервые теорию такого распада создал российский ученый Гамов, объяснивший
- частицы. Впервые теорию такого распада создал российский ученый Гамов, объяснивший 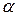 - распад в терминах туннелирования
- распад в терминах туннелирования 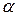 - частицы из потенциальной ямы, которой для неё является ядро.
- частицы из потенциальной ямы, которой для неё является ядро.
Теперь нам важно подчеркнуть, что при автоэлектронной эмиссии (как и в случае туннельного эффекта) имеется именно пространственный потенциальный барьер. Однако потенциальные барьеры бывают и иного рода. Например, запрещенная зона  между валентной зоной и зоной проводимости или энергетическое расстояние между разрешенными уровнями атома, так же могут рассматриваться как потенциальные барьеры. Их особенность состоит в том, что они не имеют пространственного характера, как (2.3.3) или (1), а находятся в любой точке кристалла. В этом случае тоже возможен своеобразный туннельный эффект. Обсудим это явление на примере электрического пробоя Зинера.
между валентной зоной и зоной проводимости или энергетическое расстояние между разрешенными уровнями атома, так же могут рассматриваться как потенциальные барьеры. Их особенность состоит в том, что они не имеют пространственного характера, как (2.3.3) или (1), а находятся в любой точке кристалла. В этом случае тоже возможен своеобразный туннельный эффект. Обсудим это явление на примере электрического пробоя Зинера.
Что происходит с электроном в электрическом поле? Если электрон свободный, то, ускоряясь под воздействием силы Кулона
 (3.2.2)
(3.2.2)
(мы учли, что заряд электрона отрицательный), электрон приобретает энергию. Рост энергии ограничивается столкновениями электронов с несовершенствами кристалла или атомами в газе, но может быть весьма значительным.
Квазиэлектрон твердого тела ведет себя в электрическом поле немного иначе. Он ускоряется полем, и его энергия, а также импульс, начинают зависеть от времени. Импульс или волновое число квазиэлектрона в момент времени  равны
равны
 (3.2.3)
(3.2.3)
(время  ограничивается временем свободного пробега – временем
ограничивается временем свободного пробега – временем  между столкновениями).
между столкновениями).
Обратим теперь внимание на зависимости энергии квазиэлектрона от импульса (волнового числа) и координаты. Как отмечалось в предыдущих разделах курса ФОПИ, в силу периодичности кристаллической и обратной решеток, имеет место периодичность законов дисперсии:
 , (3.2.4)
, (3.2.4)
 , (3.2.5)
, (3.2.5)
где  – произвольное целое число,
– произвольное целое число,  – постоянная решетки в Х-направлении,
– постоянная решетки в Х-направлении,  – Х-проекция вектора обратной решетки.
– Х-проекция вектора обратной решетки.
Периодичность законов дисперсии (4) и (5) означает, что при движении в электрическом поле
энергия квазиэлектрона плавно изменяется от значения, соответствующего дну рассматриваемой зоны, до значения, соответствующего потолку зоны, затем монотонно убывает до нуля (дно зоны) и вновь возрастает до максимального значения. При этом в прямом (координатном) пространстве движение квазиэлектрона ограничено – когда энергия достигает значения максимума, возникает Брегговское отражение квазиэлектрона от решетки, и он вынужден двигаться против направления поля, то есть тормозиться. В обратной решетке этому соответствует переход квазиэлектрона из одной зоны Бриллюэна в другую.
Однако финитный характер движения квазиэлектрона (заметим, что финитность движения приводит к дополнительному квантованию энергии) строго выполняется только для модели одной разрешенной энергетической зоны. Наличие второй разрешенной зоны, приводит к изменению характера движения квазиэлектрона. В этом случае квазиэлектрон, уже получивший энергию, равную энергии потолка разрешенной зоны, имеет вероятность получить от поля дополнительную энергию порядка  и перейти в более высокую разрешенную зону (например, из валентной зоны в зону проводимости). Наглядно этот процесс можно изобразить как туннелирование между наклонными в электрическом поле разрешенными зонами. Напомним, что в равновесии зона проводимости и валентная зона изображались параллельными горизонтальными прямыми (без специфического указания координаты). При включении электрического поля и росте волнового числа согласно формуле (3), картину разрешенных зон можно изобразить параллельными, но наклонными к оси x прямыми. Для того, чтобы перейти из валентной зоны в зону проводимости квазиэлектрон должен совершить туннельный переход. Квантовомеханическое описание такого перехода приводит к вероятности междузонного перехода в постоянном электрическом поле
и перейти в более высокую разрешенную зону (например, из валентной зоны в зону проводимости). Наглядно этот процесс можно изобразить как туннелирование между наклонными в электрическом поле разрешенными зонами. Напомним, что в равновесии зона проводимости и валентная зона изображались параллельными горизонтальными прямыми (без специфического указания координаты). При включении электрического поля и росте волнового числа согласно формуле (3), картину разрешенных зон можно изобразить параллельными, но наклонными к оси x прямыми. Для того, чтобы перейти из валентной зоны в зону проводимости квазиэлектрон должен совершить туннельный переход. Квантовомеханическое описание такого перехода приводит к вероятности междузонного перехода в постоянном электрическом поле
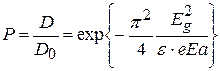 . (3.2.6)
. (3.2.6)
где  - средняя энергия квазиэлектрона (по порядку величины сравнимая с шириной запрещенной зоны
- средняя энергия квазиэлектрона (по порядку величины сравнимая с шириной запрещенной зоны  ), а – постоянная решетки в направлении действия поля.
), а – постоянная решетки в направлении действия поля.
Вероятность (6) такого перехода достигает заметных величин, если электрон на расстоянии в одну постоянную решетки  получает от электрического поля энергию, сравнимую с шириной запрещенной зоны. Такие переходы приводят к появлению электронов проводимости, которые формируют сильный ток с большими джоулевыми потерями. Выделяющееся при этом тепло приводит к механическому разрушению образца, в связи с чем явление получило название электрический (или туннельный) пробой Зинера. Пробой Зинера возникает в электрических полях с напряженностью порядка 106 В/см.
получает от электрического поля энергию, сравнимую с шириной запрещенной зоны. Такие переходы приводят к появлению электронов проводимости, которые формируют сильный ток с большими джоулевыми потерями. Выделяющееся при этом тепло приводит к механическому разрушению образца, в связи с чем явление получило название электрический (или туннельный) пробой Зинера. Пробой Зинера возникает в электрических полях с напряженностью порядка 106 В/см.
В таких же полях наблюдается другой эффект. Он аналогичен эффекту Штарка (смещение энергетических уровней в электрическом поле) и заключается в относительном сдвиге зоны проводимости и валентной зоны с изменением  . Это эффект Франца – Келдыша.
. Это эффект Франца – Келдыша.
|
|
