Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Лекция №27

Движущей силой процесса массопереноса в фазах (жидкой и газообразной) является разность равновесной концентрации и текущей концентрации.

равновесные концентрации компонента в газообразной и жидкой фазе;

y, x – текущее (рабочее) значение концентраций.

– равновесная концентрация компонента в газообразной фазе, если концентрация компонента в жидкой фазе равна x.

Рисунок 171. Иллюстрация равновесия пара над жидкостью.

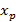– равновесная концентрация компонента в газообразной фазе, если концентрация компонента в жидкой фазе равна y.

Рисунок 172. Иллюстрация равновесия жидкости под паром.

Чтобы рассчитать систему массопереноса в фазах, необходимо знать:

1) Свойства вещества для определения равновесных концентраций (прежде всего кривую упругости, т.е. зависимость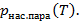

Обычно концентрации или доли для насыщенного состояния прямо пропорционально давлению насыщенного пара.

2) Условие фазового равновесия, т.е. значение параметров, характеризующих смесь p, T, C при которых не происходит перенос массы из жидкой фазы в газ и наоборот при адиабатных условиях.

3) Действительные рабочие концентрации, которыми обладает смесь в отдельных частях массообменного аппарата.

-равновесные: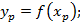

-рабочие:

Физические свойства вещества – определяют равновесные концентрации. Обычно для реальных веществ получить аналитически уравнение невозможно, поэтому реальные свойства вещества идеализируются, исходя из некоторых допущений.

Рассматриваем бинарный раствор, обладающий идеальными свойствами в газовой и жидкостной фазе, поэтому можно использовать закон Дальтона и Рауля. Для условия равновесия прежде всего важно равенство T жидкой и газообразной фазы для бинарного раствора. Общее давление в газовой фазе равно сумме парциальных давлений первого и второго компонента в газовой фазе.

Рисунок 173. Иллюстрация равновесия бинарной смеси

;

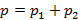объемные концентрации компонентов в газовой фазе.

Т.к.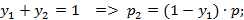

Применение закона Рауля.

- устанавливает соответствие между давлением пара над жидкостной смесью в зависимости от концентрации данного компонента в жидкости:

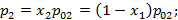
Где давления насыщенного пара первого и второго компонента смеси при данной температуре.

Исходя из законов Дальтона и Рауля можно записать зависимость давления газовой смеси от концентраций компонентов в жидкости:

В результате получаем следующую систему:

Поэтому если знаем T и p газовой смеси, можно однозначно определить концентрации компонентов в жидкой и газообразной фазах, поскольку и 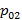зависят только от температуры.

Бинарную смесь определяют 4 параметра: p, T, x, y.

Поэтому по правилу Гиббса число независимых переменных для бинарной смеси, находящихся в жидком и газообразном состояниях, будет равно:

Поэтому нужно знать 2 любых неизвестных, чтобы определить остальные 2.

Общее давление газовой смеси обычно определяют как функцию концентрации компонента в жидкости для заданной константы температуры.

Рисунок 174. p-x диаграмма для бинарной смеси.

Если ;
Если .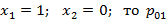

Низкокипящий: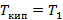

Высококипящий: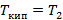

.

Если

Пример:

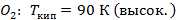
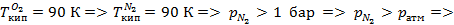
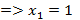- чистый низкокипящий компонент, а 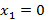- чистый высококипящий компонент с давлением насыщенного пара меньше, чем у низкокипящего при одинаковой температуре.

Найдем соотношение между концентрациями низкокипящего компонента в газовой и жидкой фазах:

;

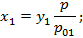
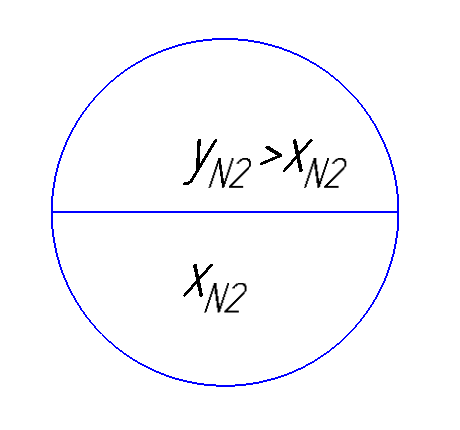
Рисунок 175. T-x, y диаграмма для бинарной смеси азот-кислород.

Для смеси .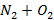

В жидкости концентрации низкокипящего компонента будет меньше, чем в газовой фазе, поскольку он более интенсивно испаряется по сравнению с высококипящим компонентом при p, T = const для воздуха, который можно представить в виде бинарной смеси концентрация в паровой фазе будет выше, чем в жидкой и поэтому равновесная концентрация будет больше концентрации в жидкой фазе.

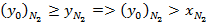
При дальнейшем рассмотрении бинарных смесей под x будем подразумевать концентрацию низкокипящего компонента в жидкой, а под y – концентрацию низкокипящего компонента в паровой фазе.

концентрации высококипящего компонента в жидкой и паровой фазах.

Если y = x для смеси, то такая смесь называется азеотропной, и методомнизкотемпературной ректификации ее разделить нельзя.

Процесс разделения с помощью ректификации основан на том, что концентрация низкокипящего компонента в паровой фазе будет выше, чем концентрация низкокипящего компонента в жидкости.

Найдем соотношение между равновесной концентрацией низкокипящего компонента в газовой фазе и концентрации этого компонента в жидкой фазе.

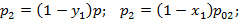
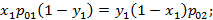
коэффициент летучести, равный отношению равновесного давления низкокипящего компонента к равновесному давлению высококипящего компонента при той же температуре.

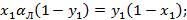
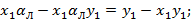
Если

Зависимость имеет гиперболический вид, т.е. с увеличением x, y уменьшается.

Для реальных веществ это уравнение несправедливо, поскольку не учитывает специфику каждой индивидуальной смеси, поэтому для расчетов используются таблицы или диаграммы для реальных смесей (растворов). Обычно используются следующие 4 диаграммы, которые дают зависимости параметров смеси от концентрации низкокипящего компонента в жидкости:

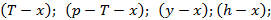
Диаграмма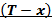

Рисунок 176. T-x, y диаграмма для бинарной смеси азот-кислород.

T₁, T₂ – температуры кипения (конденсации) низкокипящего и высококипящего компонента.

С ростом давления линии конденсирования и кипения поднимаются вверх:

С помощью диаграммы можно определить равновесные концентрации для данной p, T в паровой и жидкой фазах.

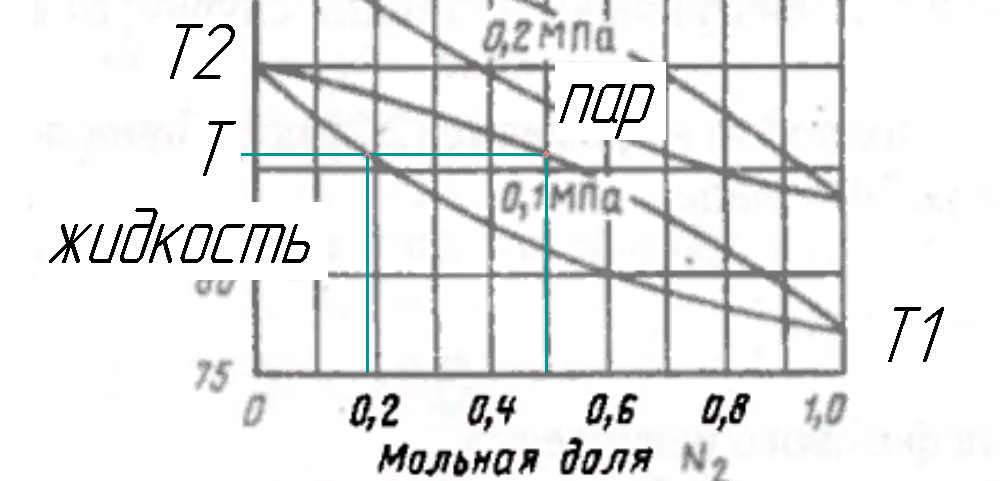
Рисунок 177.Определение состояния на T-x, y диаграмме по температуре.

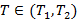
Зависимость от p.

Рисунок 178. Зависимость кривых равновесия от давления.

С ростом давления линии кипения и конденсации смеси сближаются друг с другом, в результате с ростом давления разность между концентрациями низкокипящих компонент в паре и жидкости уменьшается => уменьшается движущая сила процесса газовой смеси и сметь при высоких давлениях разделить труднее, чем при низких.

Поэтому используют по возможности минимальное давление для разделения газовой смеси.

Диаграмма

Рисунок 179. У-х диаграмма для низкокипящего компонента.

С ростом давления зависимость y(x) приближается к прямой y = x.

Точка (x=0, y=0) будет соответствовать чистому высококипящему компоненту;

(x=1, y=1) – чистому низкокипящему компоненту.

Поскольку движущая сила процесса 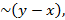то:

Графически (y - x) равен вертикальному отрезку между зависимостью и y = x, поэтому чем дальше зависимость от y = x, т.е. давление процесса меньше, тем более эффективно разделить данную смесь.

При больших давлениях для разделения требуется либо больше времени процесса, либо большая поверхность массообмена.

При расчете тройной смеси (N₂ - О₂ – Ar) можно использовать диаграммы бинарной смеси (N₂- О₂), и для получения более точных оценок необходимо использовать либо диаграмму тройной смеси или при использовании бинарной смеси занижать коэффициент эффективности процесса разделения.

Диаграмма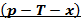

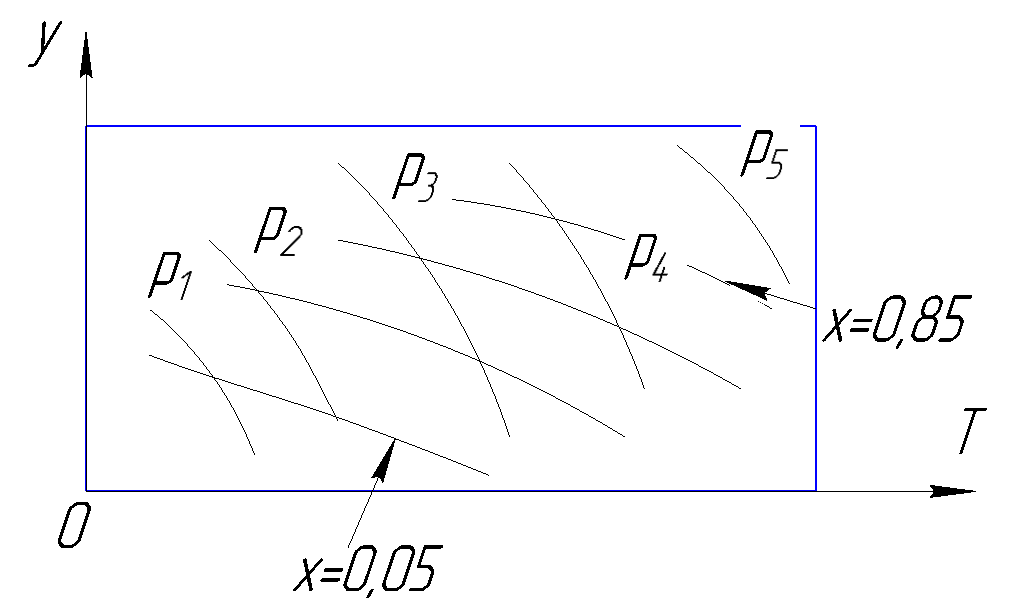
Рисунок 180. У-T диаграмма.

С помощью данной диаграммы можно, зная 2 параметра из 4, определить два остальных.

Рисунок 181.Определение состояния по у-T диаграмма.

Диаграмма

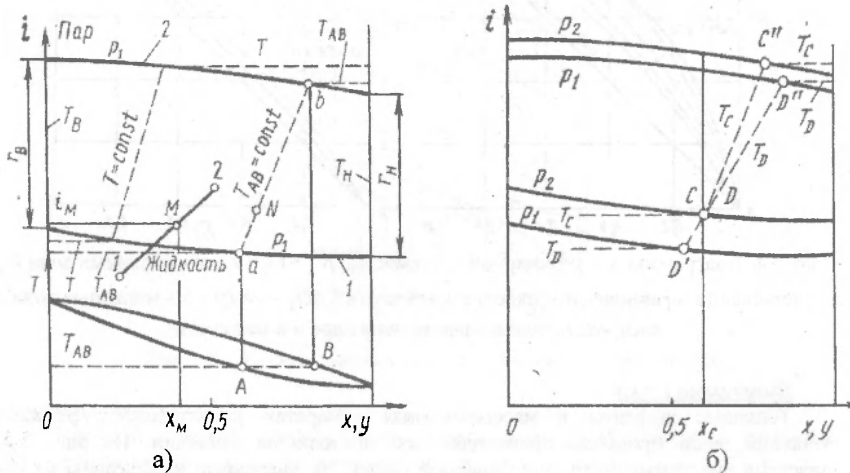
Рисунок 182. i-x диаграмма.

Зависимость от p: с ростом давления линии кипения и конденсации смещаются вверх.

С помощью этой диаграммы можно рассмотреть процесс дросселирования.

При дросселировании жидкой смеси, находящейся в состоянии насыщения получается парожидкостная смесь с уменьшением низкокипящего компонента в жидкой фазе и увеличением низкокипящего компонента в паровой фазе.

Чем больше величина концентрации низкокипящего компонента, тем труднее его разделить, в том числе и с помощью дросселирования, поскольку изотермы в h-x диаграмме идут более круто в двухфазной области при больших значениях x.

Изображение смешений смесевых поток на h-x диаграмме

Рисунок 183. Смешение на i-x диаграмме.

Смешиваем два потока или два вещества, которые характеризуются точками 1 и 2.

– количество первого и второго вещества, [моль]; -

Используем законы сохранения масс и энергии:

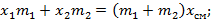
В результате точка смешения лежит на прямой, проходящей через точки, характеризующих параметры смешивающихся веществ на диаграмме, причем положение точки смешения определяется соотношениями между массами смешиваемых веществ.

Из закона сохранения энергии имеем:

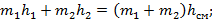
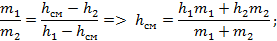
В результате смешения жидкости и влажного пара – также получаем влажный пар с большим количеством жидкости. Проведя через точку смешения изотерму, можно определить концентрации низкокипящего компонента в жидкой и паровой фазах.

Испарение бинарного раствора.

Может проводиться без отбора получившегося пара или с непрерывным отбором пара.

1) Без отбора

Рисунок 184. Испарение бинарного раствора.

m – количество жидкости;

V – количество пара;

x₀ – начальная концентрация низкокипящего компонента в жидкой фазе.

В процессе испарения количество жидкости уменьшается, количество пара возрастает. Поскольку пар не отводится, то общее кол-во пара и жидкости остается постоянным.

Зависимость количества жидкости от концентрации (мольной доли) определяется из уравнения материального баланса по низкокипящему компоненту в начале и в конце процесса.

Рассмотрим изменения концентраций низкокипящего компонента.

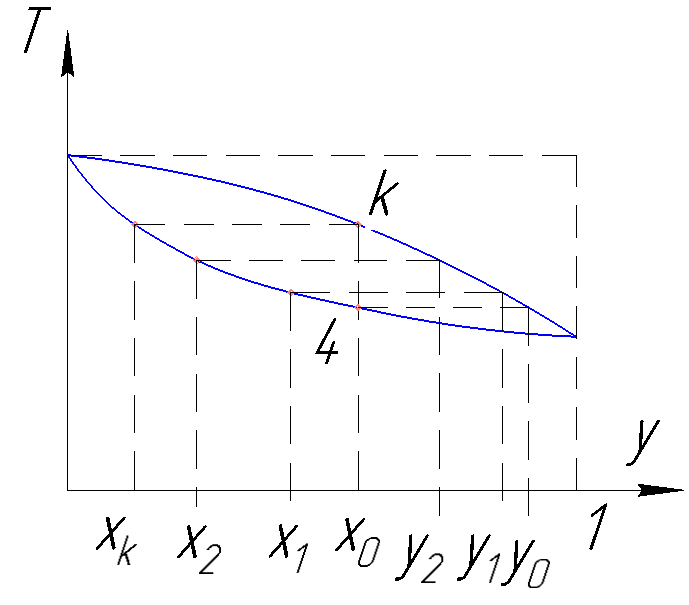
Рисунок 185. Испарение бинарного раствора.

1) В начальный момент кипения имеем максимальное кол-во низкокип.комп.в паре;

2)

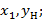
3) С течением времени при кипении концентрация низкокипящего компонента в паровой и жидкостной фазах уменьшается.

В конечной точке, когда последняя капля превращается в пар, имеем наинизшую концентрацию низкокипящего компонента в последних каплях жидкости.

Например, для воздуха, как бинарная смесь:

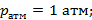
= > получать чистые продукты без отвода пара невозможно, поскольку концентрации низкокипящего компонента в начале процесса в жидкостной фазе равна концентрации в конце процесса в паровой фазе.

2) С отводом пара.

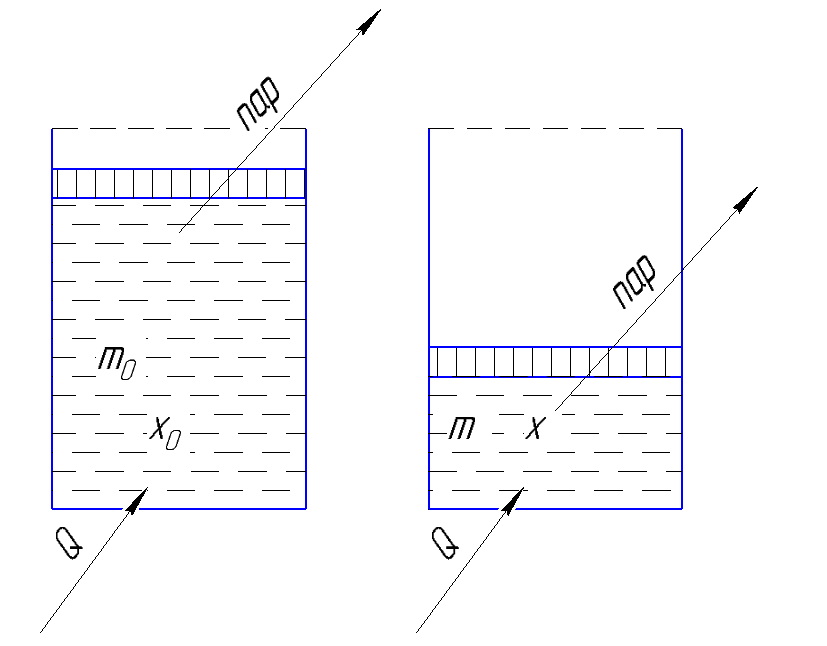
Рисунок 186. Испарение бинарного раствора с отводом пара.

В исходном состоянии жидкость имела массу М₀, и х₀ – начальная концентрация низкокипящего компонента. В результате через 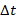ушло в пар dM, масса стала М, концентрация х.

Запишем уравнение закона сохранения массы для процесса испарения по низкокипящему компоненту.

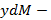ушло в пар низкокипящего компонента;

– из жидкости ушло низкокипящего компонента.

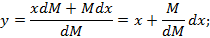
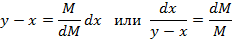
Считаем процесс испарения равновесным, т.е. для данной температуры и давления концентрация низкокипящего компонента в паровой фазе равна равновесной концентрации, которая зависит от концентрации низкокипящего компонента в жидкости.

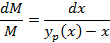
Поскольку 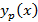имеет существенно нелинейный характер, то решить данное дифференциальное уравнение можно только численными методами

Рассмотрим данный процесс испарения в координатах (Т-х).

При использовании этого метода испарения жидкости выводится низкокипящий компонент и она обогащается высококипящим. Таким образом осуществляя кипение с непрерывным отводом пара можно получить сколь угодно чистую жидкость, состоящую преимущественно из высококипящего компонента.

Рисунок 187. Испарение бинарного раствора с отводом пара.

Для определения количества оставшейся жидкости в зависимости от концентрации низкокипящего компонента в жидкости традиционно используют графическое численное решение на диаграмме (y-x):

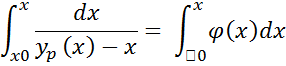
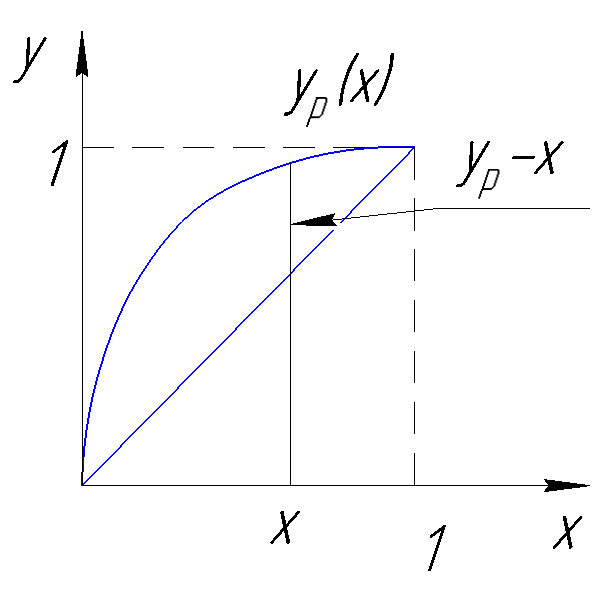
Рисунок 188. Определение количества оставшейся жидкости по y-x диаграмме.

Рисунок 189. Определение количества оставшейся жидкости по y-x диаграмме.

В результате получаем жидкость, обогащенную высококипящим компонентом.

Аналогичный, но обратный процесс будем иметь при конденсации бинарной смеси с непрерывным отводом жидкости. В этом случае пар с течением времени будет обогащаться низкокипящим компонентом.

Рисунок 190. Конденсирование с отводом жидкости.