Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Уравнение непрерывности тока

В общем случае, для полупроводника, в объеме которого происходит генерация (G) и линейная рекомбинация, изменение концентрации носителей во времени заряда может быть определено в результате решения уравнения непрерывности:

	(3.30)
	(3.31)

в одномерном случае:

	(3.32)
	(3.33)

Если генерация в объеме отсутствует и, учитывая уравнения (3.28), получим:

	(3.34)
	(3.35)

Если напряженность электрического поля не зависит от координаты:

	(3.36)
	(3.37)

Если напряженность электрического поля не зависит от координаты ее можно определить, с помощью уравнения Пуассона, определяющего связь между распределением заряда и электрическим полем в образце:

(3.38)

Заряд определяется уравнением электронейтральности

().В трехмерном случае .

Уравнения (3.36-3.38) устанавливают связь между концентрацией носителей заряда и основными, влияющими на них, процессами: диффузией, дрейфом, генерацией и рекомбинацией. Они позволяют по известным значениям потенциала (или напряженности поля) рассчитать пространственное распределение носителей заряда и его изменение со временем.

Полупроводниковые приборы состоят, в основном из легированных областей p - или n -типа, при низких напряженностях электрического поля (при низких уровнях инжекции) концентрация основных носителей изменяется слабо, поэтому характер протекающих в этих материалах процессов будет определяться, в основном, неосновными носителями заряда.

В стационарных условиях ()и при отсутствии внешнего электрического поля ( =0) уравнения напрерывности примут вид:

для n-типа: для p- типа: .

(3.39)

Пусть в образце n -типа избыточные носители инжектируются с одной стороны образца, при этом напряжение смещения отсутствует. В этом случае мы имеем одномерное уравнение непрерывности:

.

(3.40)

Его решение должно удовлетворять граничным условиям и , имеет вид .

Диффузионные длины для электронов L_n и для дырок L_p характеризуют то расстояние, на которое в результате диффузии проникнут неосновные носители, не прорекомбинировав с основными, то есть за время жизни. .

Изменим теперь второе граничное условие, полагая, что все избыточные носители удаляются из образца при , т.е. . В этом случае решением уравнения (3.40) является функция

.

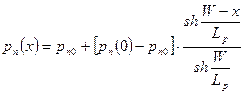(3.41)

С помощью уравнения (3.25) можно рассчитать плотность дырочного тока при :

.

(3.42)

Уравнения (3.41), (3.42) будут широко использоваться при анализе процессов в таких полупроводниковых приборах, как биполярные транзисторы и диоды. Причем для p – области будем использовать уравнение для неосновных носителей – электронов, для n – области для дырок. Уравнение для носителей противоположного знака решать не будем, полагая, что соблюдается условие квазиэлектронейтральности и Δ p = Δ n.