Електростатичне поле у вакуумі, його потенціальність. Принцип суперпозиції і теорема Гаусса. Енергія взаємодії системи зарядів і енергія електростатичного поля.

Якщо заряди розмістити у вакуумі, то сили їх взаємодії зменшаться. Закон взаємодії нерухомих точкових зарядів у вакуумі називається законом Кулона. Він формулюється так: сила взаємодії F двох нерухомих точкових зарядів у вакуумі прямо пропорційна добуткові цих зарядів q₁ i q₂, і обернено пропорційна квадратові відстані r між, ними і напрямлена вздовж прямої, яка сполучає ці заряди, тобто k – коеф. пропорційності. Сили взаємодії однойменних зарядів є силами відштовхування, а різнойменних – силами притягання. Сили відштовхування вважають додатними, сили притягання – від’ємними.

Принцип суперпозиції: сила, що діє на певний точковий заряд з боку інших точкових зарядів, дорівнює векторній сумі сил, що діють на нього з боку цих зарядів: де r_i0 – радіус-вектор проведений від q_iдо q_0.

Для точкового заряду напруженість поля визначається як: .

Якщо точкових зарядів декілька, то:

Теорема Гаусса пов’язує потік вектора напруженості електростатичного поля через довільну замкнену поверхню із зарядом, який охоплюється нею.Потік вектора напруженості через елемент площадки dS: E_n – проекція Е на нормаль n, α – кут між нормаллю і Е. Повний потік через поверхню S: Для точкового заряду: dΩ – елемент тілесного кута.

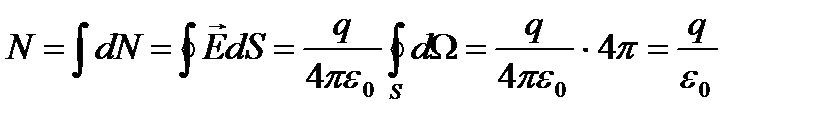
Теорема Гауса для системи точкових зарядів: потік вектора напруженості електростатичного поля у вакуумі через довільну замкнену поверхню зсередини назовні дорівнює алгебраїчній сумі тих точкових зарядів, які охоплюються поверхнею S, поділеній на електричну сталу:

Якщо заряди розподілені неперервно і вони обє’мні, то:

Енергія взаємодії точкових зарядів визначається як:

Енергія електростатичного поля:

3.3.2 Постійне магнітне поле у вакуумі, його вихровий характер. Закон Біо-Савара-Лапласа і теорема про циркуляцію. Енергія магнітного поля.

Маг-поле вид матерії, складова частина електро-маг поля, яка діє на рух заряджених тіл, або тіла, які мають магнітний момент, не залежно чи рухомі чи не рухомі. Воно вихрове, без джерельне. Магнітні силові лінії завжди замкнені, ніде не починаються і не закінчуються. Магнітне поле є навколо рухомих зарядів. Магнітна силова лінія – це лінія дотична до якої в кожній точці збігається за напрямом з силою, що діє в цій точці.

Оскільки магнітні силові лінії замкнені то робота, яка виконується при переміщенні провідника зі струмом у магнітному полі по замкненому контурі не дорівнює 0.

Оскільки характеристикою магніт поля є вектор магнітної індукції, напрям і величину вектора магнітної індукції визначають за дією магнітного поля на магнітну стрілку та провідник із струмом і напрям магнітної індукції в заданій точці приймають напрям сили, з якою магнітне поле діє на північний полюс нескінченно малої магнітної стрілки, розміщеної в даній точці. Біо і Савар намагалися знайти загальний закон, який дав би змогу обчислити магнітну індукцію в кожній точці поля створеного електричним струмом, що протікає по провіднику будь-якої форми. Це зробив Лаплас. Він врахував векторний характер магнітної індукції і висловив важливу гіпотезу про те, що індукція В у кожній точці маг поля будь-якого провідника зі струмом = векторній сумі індукцій 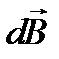елементарних магнітних полів, створюваних кожною ділянкою dl цього провідника. Закон Біо-Савара-Лапласа: 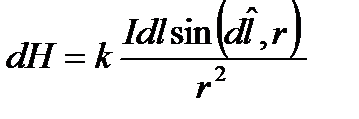- індукція вдеякій точці А провідника із струмом; 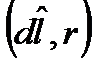- кут між векторами 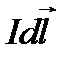і напрямом струму ; k- коефіцієнт пропорційності, який залежить від вибору одиниць 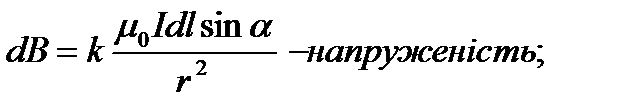де H, береться тому що від форми провідника тої самої довжини буде різна напруженість поля – поля суперпозуються: циркуляція вектора напруженості маг поля по довільно замкнутому контурі =алгебр сумі струмів, що охоплюється цим контуром.

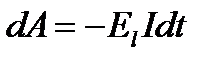
В процесі наростання струму джерело сторонніх сил викон роботу проти сил ЕРС самоіндукції. За час сила струму викон роботу . Зміна електр-маг поля пов’язана зі зміною магнітного потоку:
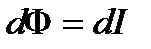