
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Операторы и функции в MATLAB.
|
|
Основные операторы: арифметические, логические и операторы отношений.
Число арифметических операторов в MATLAB достаточно большое и включает в себя следующие арифметические операции:
– сложение (М1+М2); – вычитание (М1-М2); – умножение (М1*М2); – возведение в степень (М1 ^ ); – возведение матрицы в степень (М1Ù х); – поэлементное возведение массива в степень (М1.Ù х);
– деление матриц слева направо (М1 / М2); – деление матриц справа налево (М1 \ М2).
Операторы отношения служат для сравнения двух величин, векторов или матриц, все операторы отношения имеют две сравниваемые величины и записываются в следующем виде:
– равно (х = = у); – не равно (х ~ = у); – меньше (х < у); – больше (х > у); – меньше или равно (х < = у); – больше или равно (х > = у).
Данные операторы выполняют поэлементное сравнение векторов или матриц одинакового размера и логическое выражение принимает значение 1 (True), если элементы идентичны, и значение 0 (False) в противном случае.
Логические операторы служат для реализации поэлементных логических операций над элементами одинаковых по размеру массивов:
– логическое И (and (a, b)); – логическое ИЛИ (or (a, b)); – логическое НЕ (not (a, b));
– исключающее ИЛИ (xor (a, b)); – верно, если все элементы вектора равны нулю (any (a));
– верно, если все элементы вектора не равны нулю (all (a)).
В Matlab приоритет логических операций выше, чем арифметических, приоритет возведения в степень выше приоритетов умножения и деления, приоритет умножения и деления выше приоритета сложения и вычитания. Для изменения приоритета операций в математических выражениях используются круглые скобки. Степень вложения скобок не ограничивается.
Функция – это имеющий уникальное имя объект, выполняющий определенные преобразования своих аргументов и при этом возвращающий результаты этих преобразований. Функции в общем случае имеют список аргументов (параметров), заключенный в круглые скобки. Имена встроенных (стандартных) функций записываются строчными буквами.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
Условный оператор if в MATLAB записывается в общем виде так:
| if Логическое условие Оператор 1 elseif Логическое условие Оператор 2 else Оператор 3 end; |
Эта конструкция имеет несколько частных вариантов:
| if Логическое условие Оператор 1 end; |
| if Логическое условие Оператор 1 else Оператор 2 end; |
Логическое условие записывается в виде:
| Выражение 1 Оператор отношения Выражение 2 |
Как и в других алгоритмических языках, оператор if позволяет осуществить разветвление процесса вычислений в зависимости от какого-либо условия.
Набор элементарных функций (все элементарные функции должны записываться в программах малыми буквами)
представим их описанием, причем в тригонометрических функциях углы измеряются в радианах:
– ê х ê (модуль) abs (x); – ех (экспонента) exp (x); –  (натуральный логарифм) log (x)
(натуральный логарифм) log (x)
–  (логарифм по основанию 2) log 2(x); –
(логарифм по основанию 2) log 2(x); – 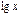 (десятичный логарифм) log 10(x)
(десятичный логарифм) log 10(x)
– 2 х (2 в степени х) pow (x); –  (квадратный корень) sqrt (x); – arcсos x (арккосинус) acos (x); – arсctg x (арккотангенс) acot (x); – arcсosec x (арккосеканс) acsc (x); – arcсes x (арксеканс) asec (x); – arcsin x (арксинус) asin (x)
(квадратный корень) sqrt (x); – arcсos x (арккосинус) acos (x); – arсctg x (арккотангенс) acot (x); – arcсosec x (арккосеканс) acsc (x); – arcсes x (арксеканс) asec (x); – arcsin x (арксинус) asin (x)
– arсtg x (арктангенс) atan (x); – сos x (косинус) cos (x); – ctg x (котангенс) cot (x); – sec x (секанс) sec (x)
– сosec x (косеканс) csc (x); – sin x (синус) sin (x); – tg x (тангенс) tan (x); – arсch x (арккосинус гиперболический) acosh (x)
– arсcth x (арккотангенс гиперболический) acoth (x); – arссosech x (арккосеканс гиперболический) acsch (x)
– arсsech x (арксеканс гиперболический) asech (x); – arсsh x (арккосинус гиперболический) asinh (x)
– arсtgh x (арктангенс гиперболический) atanh (x); – ch x (косинус гиперболический) cosh (x)
– сtgh x (котангенс гиперболический) coth (x); – сosech x (косеканс гиперболический) csch (x)
– sech x (секанс гиперболический) sech (x); – sh x (синус гиперболический) sinh (x)
– tgh x (тангенс гиперболический) tanh (x);
|
|
