Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Составляющей решения дифференциального уравнения

Если правая часть дифференциального уравнения имеет вид

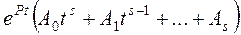, (П 1.1)

то, если 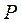не является корнем характеристического уравнения, вынужденную составляющую надо искать в таком же виде

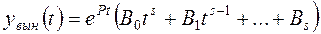. (П 1.2)

Если же 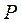является корнем характеристического уравнения кратности 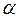, то 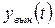надо искать в виде

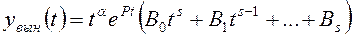. (П 1.3)

Пример П 1.1. [6, с. 127].

.

Вынужденную составляющую надо искать в виде

.

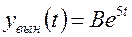Пример П 1.2. [6, с. 127].

.

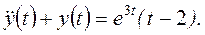Вынужденную составляющую надо искать в виде

.

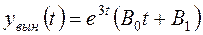Пример П 1.3. [6, с. 127].

.

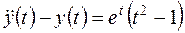Вынужденную составляющую надо искать в виде

,

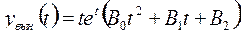так как 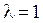является корнем характеристического уравнения.

Пример П 1.4. [6, с. 127].

.

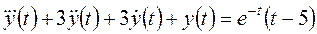Вынужденную составляющую надо искать в виде

,

так как 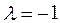является корнем характеристического уравнения.

Если правая часть дифференциального уравнения имеет вид

, (П 1.4)

где один из многочленов 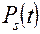или 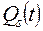имеет степень 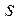, а другой – степень не выше чем 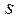, то

– если 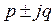не является корнями характеристического уравнения

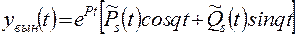, (П 1.5)

где 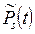, 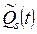– многочлены степени 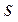с неопределенными коэффициентами;

– если 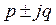являются 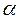– кратными корнями характеристического уравнения

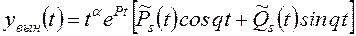. (П 1.6)

Пример П 1.5. [6, с. 128].

; .

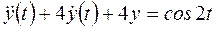Так как числа 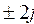не являются корнями характеристического уравнения, то 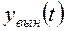надо искать в виде

.

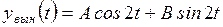Пример П 1.6. [6, c.128].

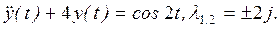
Так как числа ±2j являются простыми корнями характеристического уравнения, то 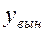надо искать в виде

Пример П 1.7. [6, c.128].

Так как числа ±j являются двукратными корнями характеристического уравнения, то 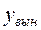надо искать в виде

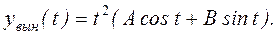
Пример П 1.8. [6, c.128].

Так как -1±j являются простыми корнями характеристического уравнения, то 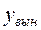надо искать в виде