Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

В анализе линейных стационарных систем

Сущность метода заключается в следующем. Пусть задана некоторая функция , причем такая, что для нее существует преобразование Лапласа ( -преобразование)

,

то есть интеграл в правой части этого равенства является сходящимся.

- называется оригиналом, а - изображением. При переходе от оригиналов к изображениям операции дифференцирования и интегрирования заменяются операциями соответственно умножения и деления изображений на . Это позволяет дифференциальное уравнение относительно заменить на алгебраическое уравнение относительно . Решив это алгебраическое уравнение и найдя , получим изображение решения исходного дифференциального уравнения.

Для определения самого решения можно использовать обратное преобразование Лапласа

,

где .

Для нахождения 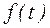можно во многих случаях избежать непосредственного вычисления интеграла, воспользовавшись таблицей соответствий “оригинал - изображение” (приложение 2). Метод анализа систем (решение обыкновенных дифференциальных уравнений) сводится к следующей схеме, рис. 3.

При исследовании одномерных систем применение преобразования Лапласа основано на переходе от модели в форме дифференциального уравнения к модели в форме передаточной функции.

Пространство оригиналов	Уравнение относительно f(t) и начальные условия		Искомая функция
Пространство изображений	Алгебраическое уравнение относительно изображения F(s)	Þ	Изображение F(s)

Рис.3

Пример 6 [4, c.146]. Математическая модель системы имеет вид:

Начальное состояние системы:

Определить свободную составляющую движения системы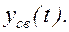

Считаем u(t)=0 (так как определяется ) и преобразуем каждый член уравнения по Лапласу:

После преобразования по Лапласу исходное дифференциальное уравнение сделается алгебраическим относительно изображения:

Откуда

Знаменатель этой дроби (характеристическое уравнение) имеет корни (собственные числа):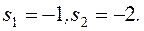

Поэтому

Для определения оригинала соответствующего изображению 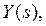находим обратное преобразование Лапласа (приложение 2):

Пример 7. Для электрической схемы, рис.1, определить закон изменения тока, соответствующий изменению e(t)=t в. Начальные условия Параметры схемы

Математическая модель схемы в данном случае принимает вид:

1 способ решения.

Характеристическое уравнение:

Собственные числа: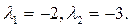

Поэтому

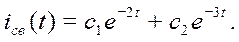
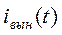определенное, например, по виду правой части имеет вид

.

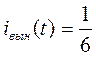Следовательно,

Постоянные определим из начальных условий

Окончательно закон изменения тока в схеме имеет вид

2 способ решения.

Вычислим преобразование Лапласа от обеих частей дифференциального уравнения (модели схемы):

Далее

Вычислив оригинал (приложение 2), получим:

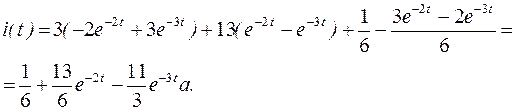
Таким образом, оба способа решения дали одинаковый результат, что и следовало ожидать.

Пример 8. Математическая модель системы имеет вид:

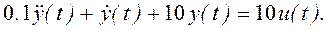
Определить переходную функцию h(t), то есть закон изменения выходной переменной при подаче на вход системы воздействия в виде единичной ступенчатой функции u(t)=1(t), начальные условия нулевые.

1 способ.

Определим

Характеристическое уравнение:

Собственные числа:

Поэтому

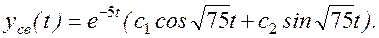
Определим

определяем по виду правой части (приложение 2), .

Следовательно,

Постоянные 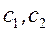определяются из начальных условий

Окончательно,

2 способ.

Модель системы в форме передаточной функции имеет вид:

Так как

то .

Проведем следующие преобразования:

Неизвестные коэффициенты определим из равенства

или

Приравнивая коэффициенты при одинаковых степенях 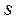, получим систему уравнений

Таким образом,

Поэтому

.

Для нахождения оригиналов запишем знаменатель в виде

.

Теперь

.

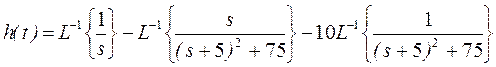По формулам приложения 2 имеем

Окончательно,