Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Взаимное расположение прямых в пространстве.

Прямую линию в пространстве следует представлять абсолютно аналогично: мысленно отмечаем две точки в пространстве и проводим с помощью линейки линию от одной точки до другой и за пределы точек в бесконечность.

Все обозначения точек, прямых и отрезков в пространстве аналогичны случаю на плоскости.

Вообще, прямая линия целиком принадлежит некоторой плоскости в пространстве. Это утверждение вытекает из аксиом:

- через две точки проходит единственная прямая;

- если две точки прямой лежат в некоторой плоскости, то все точки прямой лежат в этой плоскости.

Существует еще одна аксиома, которая позволяет рассматривать прямую в пространстве как пересечение двух плоскостей: если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.

Во-первых, две прямые могут совпадать, то есть, иметь бесконечно много общих точек (по крайней мере две общие точки).

Во-вторых, две прямые в пространстве могут пересекаться, то есть, иметь одну общую точку. В этом случае эти две прямые лежат в некоторой плоскости трехмерного пространства. Если две прямые в пространстве пересекаются, то мы приходим к понятию угла между пересекающимися прямыми.

26.ОБЪЁМ ПИРАМИДЫ.

Пирамидой называют многогранник, основанием которого является произвольный многоугольник, а все грани представляют собой треугольники с общей вершиной, являющейся вершиной пирамиды.
Пирамида – это объемная фигура. Именно поэтому довольно часто требуется найти не только ее площадь, но и объем. Формула объема пирамиды очень проста:

V= *S*h.

где S – площадь основания, а h – высота пирамиды.

29.ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ…

Производной функции называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю:

f’(x) = ;

Исходя из этого определения, рассмотрим, каким образом производная функции y=f(x) связана с графиком этой функции.

Геометрический смысл производной.

Тангенс угла наклона касательной (угловой коэффициент наклона касательной), проведенной к графику функции y=f(x) в точке 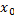равен производной функции y=f(x) в этой точке:

k = tg = f’().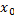

Заметим, что угол - это угол между прямой и положительным направлением оси ОХ.

Уравнение касательной к графику функции y=f(x) в точке 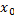имеет вид:

y= f(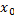) + f’(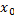)*(x- )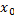

В этом уравнении:

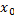- абсцисса точки касания,

f’(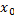) - значение функции y=f(x) в точке касания,

f’(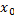) - значение производной функции y=f(x) в точке касания.