Радианная и градусная мера углов.

Для практического применения принято запоминать всего две цифры после запятой.

Запоминаем: =3, 14;

Раз уж мы поняли, что длина окружности больше диаметра в " Пи" раз, имеет смысл запомнить формулу длины окружности: L = *d;

Где L - длина окружности, а d - её диаметр.

В основе определения радиана - всё равно окружность. Угол в 1 радиан, это угол, который вырезает из окружности дугу, длина которой (L) равна длине радиуса (R).

Вот теперь совершено осмысленно можно записать приближённое равенство: 180 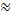3, 14;

Или точное равенство: 180 = радиан.

Определим, сколько градусов в одном радиане. Как? Легко! Если в 3, 14 радианах 180° градусов, то в 1 радиане в 3, 14 раз меньше! То есть, мы делим первое уравнение (формула - это тоже уравнение!) на 3, 14:

1 радиан = = 57, 325

16.ФУНКЦИЯ y=sinx. ЕЁ СВОЙСТВА И ГРАФИК.

Функция y=sinx определена на всей числовой прямой, является нечётной и периодической с периодом 2π.

График этой функции можно построить таким же способом, как и график функции y=cosx, начиная с построения, например, на отрезке [0; π ].

Однако проще применить формулу sinx = cos (x − ), которая показывает, что график функции y=sinx можно получить сдвигом графика функции y=cosx вдоль оси абсцисс вправо на .

Свойства функции y=sinx

1. Область определения - множество R всех действительных чисел.

2. Множество значений - отрезок [− 1; 1]

3. Функция y=sinx периодическая с периодом T=2π

4. Функция y=sinx- нечётная.

5. Функция y=sinx принимает:
- значение, равное 0, при x=π n, n∈ Z;
- наибольшее значение, равное 1, при x=π 2+2π n, n∈ Z;
- наименьшее значение, равное − 1, при x=− π 2+2π n, n∈ Z;
- положительные значения на интервале (0; π) и на интервалах, получаемых сдвигами этого интервала на 2π n, n∈ Z;

- отрицательные значения на интервале (π; 2π) и на интервалах, получаемых сдвигами этого интервала на 2π n, n∈ Z.

6. Функция y=sinx:

- возрастает на отрезке

[− ; ] и на отрезках, получаемых сдвигами этого отрезка на 2π n, n∈ Z;
- убывает на отрезке

[ ; ] и на отрезках, получаемых сдвигами этого отрезка на 2π n, n∈ Z.

17.ФУНКЦИЯ y=tgx. ЕЁ СВОЙСТВА И ГРАФИК.

Функция y=tgx определена при x≠ π 2+π n, n∈ Z, является нечётной и периодической с периодом π.

Поэтому достаточно построить её график на промежутке [0; π 2):

Выберем для построения контрольные точки, через которые проведём плавную кривую на координатной плоскости.

tg0=0;

tg = ;

tg =1;

tg = .

Затем, отобразив её симметрично относительно начала координат, получим график на интервале (− ; ).

Используя периодичность, строим график функции y=tgx на всей области определения.

График функции y=tgx называют тангенсоидой.

Главной ветвью графика функции y=tgx обычно называют ветвь, заключённую в полосе (− ; ).

Свойства функции y=tgx:

1. Область определения - множество всех действительных чисел x ≠ +π n, n∈ Z;

2. Множество значений - множество R всех действительных чисел;

3. Функция y=tgx периодическая с периодом π;

4. Функция y=tgx нечётная;

5. Функция y=tgx принимает:

- значение 0, при x= , n∈ Z;

- положительные значения на интервалах (; + ), n∈ Z;

- отрицательные значения на интервалах (− π 2+π n; π n), n∈ Z.

6. Функция y=tgx возрастает на интервалах (− + ; + ), n∈ Z.

18.ФУНКЦИЯ y=cosx. ЕЁ СВОЙСТВА И ГРАФИК.

Функция y=cosx определена на всей числовой прямой и множеством её значений является отрезок [− 1; 1]

Следовательно, график этой функции расположен в полосе между прямыми y=− 1 и y=1

Так как функция y=cosx периодическая с периодом 2π, то достаточно построить её график на каком-нибудь промежутке длиной 2π. Пример на отрезке − π ≤ x≤ π, тогда на промежутках, получаемых сдвигами выбранного отрезка на 2π n, n∈ Z, график будет таким же.

Функция y=cosx является чётной. Поэтому её график симметричен относительно оси Oy.

Для построения графика на отрезке − π ≤ x≤ π достаточно построить его для 0≤ x≤ π, а затем симметрично отразить его относительно оси Oy.

Найдём несколько точек, принадлежащих графику на этом отрезке 0≤ x≤ π cos0=1;

cos = ;

cos = ;

cos = ;

cos =0;

cosπ =− 1.

Свойства функции y=cosx:

1. Область определения - множество R всех действительных чисел;

2. Множество значений - отрезок [− 1; 1];

3. Функция y=cosx периодическая с периодом 2π;

4. Функция y=cosx – чётная;

5. Функция y=cosx принимает:

- значение, равное 0, при x = + π n, n∈ Z;

- наибольшее значение, равное 1, при x=2π n, n∈ Z;

- наименьшее значение, равное − 1, при x=π +2π n, n∈ Z;

- положительные значения на интервале (− ; ) и на интервалах, получаемых сдвигами этого интервала на 2π n, n∈ Z;

- отрицательные значения на интервале (; ) и на интервалах, получаемых сдвигами этого интервала на 2π n, n∈ Z.

6. Функция y=cosx:

- возрастает на отрезке [π; 2π ] и на отрезках, получаемых сдвигами этого отрезка на 2π n, n∈ Z;

- убывает на отрезке [0; π ] и на отрезках, получаемых сдвигами этого отрезка на 2π n, n∈ Z.

23.ОБЪЁМ ПРЯМОЙ ПРИЗМЫ.

Призма – многогранник, составленный из двух равных многоугольников A1A2…An и B1B2 и Bn, расположенных в параллельных плоскостях, и n параллелограммов.

Если боковые ребра призмы перпендикулярны к основаниям, то призма называется прямой.Прямая призма называется правильной, если её основания – правильные многоугольники.

Теорема: Объем прямой призмы равен произведению площади основания на высоту.

24.ОБЪЁМ ПРЯМОУГОЛЬНОГО ПАРАЛЛЕПИПЕДА.

Параллелепипедом называется призма, основание которой параллелограмм.Параллелепипед имеет шесть граней, и все они — параллелограммы. Параллелепипед, четыре боковые грани которого — прямоугольники, называется прямым. Прямой параллелепипед у которого все шесть граней прямоугольники, называется прямоугольным.

Объем прямоугольного параллелепипеда равен произведению площади основания на высоту:

V = SH = abc.