Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Силовой анализ рычажного механизма

Известны следующие параметры механизма:

l_AB = 0, 36 м;

l_AD = 0, 56 м;

l_ОА = 0, 125 м;

l_ОС= 0, 25 м;

l_ВС= 0, 32 м;

q= 10кг/м;

Р=2F₁ ;

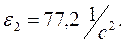
(Все ускорения берутся из первого листа курсовой работы).

Требуется определить реакции в кинематических парах и уравновешивающую силу.

Изображаем механизм в заданном положении с обозначением масштабного коэффициента

На механизм действуют следующие силы:

1.Сила полезного сопротивления , указываемая в задании. Она приложена в точке В коромысла 3 и направлена перпендикулярно ему.

2.Силы тяжести , определяемые через массы звеньев, которые можно условно найти по формуле m=ql, где q -масса единицы длины звена, l – длина звена

Следовательно,

Силы тяжести прикладываются в центрах масс S₁, S₂ , S₃ и направлены вертикально вниз.

3.Силы инерции звеньев , определяются по формулам

Эти силы прикладываются в центрах масс и направлены в стороны, обратные ускорениям .

4.Моменты сил инерции М, которые можно найти по формуле

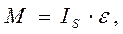
где I_S -моменты инерции звеньев относительно центральных осей.

т.к.

;

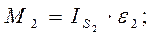
Моменты инерции звеньев определяются по формуле

Следовательно,

Моменты сил инерции М направлены в стороны, обратные угловым ускорениям.

5. Уравновешивающая сила , прикладываемая в точке

А кривошипа 1, направлена перпендикулярно ему.

Все силы и моменты указываем на механизме, причем длины векторов берем произвольно.

Изображаем отдельно структурную группу, состоящую из шатуна 2 коромысла 3. Реакции в точках А и С раскладываем на две составляющие, одну из которых направляем по звену (в ту или иную сторону), а вторую -перпендикулярно звену (так же в ту или иную строну). Из точки В на все силы проводим перпендикуляры, которые являются плечами этих сил. Замеряем каждое плечо в миллиметрах и умножаем на µ _l:

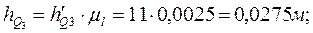
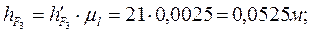
Рассматриваем равновесие звена 2, отбрасывая мысленно звено 3, и записываем уравнение моментов относительно точки В:

.

Откуда:

Отбрасываем мысленно звено 2 и записываем уравнение равновесия звена 3 относительно той же точки В:

Откуда:

Так как эта сила оказалась отрицательной, то вектор зачеркиваем и направляем в другую сторону. Используем графическое условие равновесия двух звеньев и строим силовой многоугольник в масштабе Вычисляем длины векторов сил:

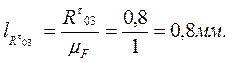
Начинаем построение с силы _, отмечая начало её точкой. Далее силы идут в любом порядке, но желательно, чтобы сначала шли все силы одного звена, а затем силы, действующие на другое звено. Последняя сила- это _. Если длина вектора одной из сил оказалась менее 3 мм, то вместо неё ставим точку с обозначением этой силы.

В начале построения к силе проводим перпендикуляр и в конце силы 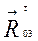также к ней проводим перпендикуляр.

Пересечение перпендикуляров дает силы _{и ,} причём сила идёт в начало силы , а вектор идет из конца силы .Таким образом, стрелки в многоугольнике идут одна за другой. Сравниваем направления векторов на чертеже и в силовом многоугольнике. Замечаем, что сила направлена в другую сторону. Поэтому её подчёркиваем и поворачиваем на 180˚.Силы в шарнирах А и С попарно складываем: _,

Сила должна идти навстречу силе _, а сила _- навстречу _. Получаем модули этих сил:

Чтобы получить реакцию в шарнире В, нужно рассмотреть равновесие одного звена, например- второго. Для этого начало силы нужно соединить с концом силы ,. Получаем вектор , который идет в начало силы 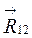. Замеряем длину этого вектора и умножаем на . Получаем модуль этой силы:

Изображаем отдельно кривошип 1 со всеми силами, причем реакцию направляем пока произвольно, а сила направлена в сторону, обратную силе , т.е. _.

Из точки О проводим перпендикуляры ко всем силам, замеряем их и умножаем на .

Получаем длины плеч сил.

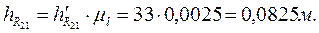
Рассматривая равновесие кривошипа, записываем уравнение моментов относительно точки О:

Строим силовой многоугольник для кривошипа в масштабе .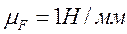

Находим длины векторов:

Замыкающий вектор многоугольника представляет собой реакцию ,

которая направлена в начало первой силы.

Измеряем длину этого вектора и умножаем на масштаб :