Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Графіки

Побудова графічної залежності між вимірюваними величинами або між вимірюваними і шуканими величинами є важливою частиною звіту. З одного боку, графіки дозволяють наочно побачити залежність між фізичними величинами. З іншого – вигляд графічної залежності у багатьох випадках дозволяє дійти висновку щодо якості проведеного експерименту.

Перед тим, як побудувати графік, слід визначити, яку величину ми будемо відкладати по осі абсцис і яку по осі ординат. Звичайно по осі абсцис відкладають незалежну змінну (час, температура, відстань, напруга і т.п.), а по осі ординат величину, яка є функцією незалежної змінної (опір провідника, сила струму, момент інерції і т.п.).

На другому етапі побудови графіка треба оцінити інтервал, в якому знаходяться значення цих величин.

Є ряд загальних правил, яких потрібно дотримуватися при побудові графіка:

1) масштаби для величин, що відкладаються по різних осях незалежні;

2) кожна вісь може починатися з нуля, або з будь-якого цілого значення;

3) масштаби слід обирати таким чином, щоб крива, що відображає шукану залежність, розташовувалася поблизу бісектриси координатного кута;

4) бажано, щоб результати вимірів на графіку були показані з тією ж точністю, з якою вони вимірювалися на досліді;

5)
графік не повинен мати вигляд ламаної лінії (рис. 4, а) бо це означало б, що при зміні однієї величини інша змінюється стрибкоподібно. Більш імовірно, що залежність має бути подібна до тієї, яка показана на рис. 4, б;

6) масштаб по осях треба обирати так, щоб залежність була чіткою (рис.5, б). При невдалому виборі масштабів наочність втрачається (рис.5, а);

7) символ величини, множник, що визначає порядок числа та одиниця виміру записуються в кінці координатної осі на вільному від експериментальних точок місці.

У багатьох випадках доводиться зображати залежність, яка має вигляд степеневої або експоненціальної функції: y = a + bx ²; y = a ·exp[ bx ]. В першому випадку зручно зображати залежність у = у (х ²), бо графік матиме вигляд прямої лінії. В другому випадку зручно зображати залежність ln y =f(x). Якщо у таких координатах ми одержимо пряму лінію, то це буде непрямим доказом справедливості експоненціальної залежності “ у ” від “ х ”.

Похибку у експериментальному значенні можна показувати на графіку таким чином:

або.

Довжина горизонтальної риски задає інтервал можливих значень для даного виміру незалежної змінної, а вертикальна – відповідний інтервал для функції.

Якщо біля експериментальної точки ми побудуємо прямокутник із сторонами 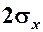та (рис. 6), то кожна точка площі цього прямокутника буде задавати значення, яке з однаковою ймовірністю належить даній залежності.

На рис. 7 зображені приклади обробки тих самих експериментальних точок, але для різних значень абсолютної похибки вимірювань. На рис.7, а абсолютна похибка досить велика, тому правомірно провести пряму лінію. У випадку, коли абсолютна похибка мала (рис. 7, б), ми повинні провести плавну криву лінію. Основною вимогою до цих ліній є те, що вони мусять перетинати всі прямокутники, побудовані навколо