💸 Как сделать бизнес проще, а карман толще?

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое раписание, но и напоминать клиентам о визитах тоже. Проблема в том, что средняя цена по рынку за такой сервис — 800 руб/мес или почти 15 000 руб за год. И это минимальный функционал. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
⚡️ Для новых пользователей первый месяц бесплатно. А далее 290 руб/мес, это в 3 раза дешевле аналогов. За эту цену доступен весь функционал: напоминание о визитах, чаевые, предоплаты, общение с клиентами, переносы записей и так далее.
✅ Уйма гибких настроек, которые помогут вам зарабатывать больше и забыть про чувство «что-то мне нужно было сделать».
Сомневаетесь? нажмите на текст, запустите чат-бота и убедитесь во всем сами!

Приклад.

В роботі досліджувався рух свинцевих кульок у гліцерині. Формула для визначення коефіцієнта динамічної в’язкості рідини має вигляд:

,

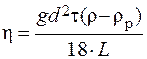де g – прискорення вільного падіння, d – діаметр кульки, r – густина свинцю, r_р – густина рідини, L – шлях, що проходить кулька за час t.

3.2. Для величин, що є сталими під час досліду прийняті такі позначення: g =9, 81 м/с², r =11350 кг/м³, r_р =860 кг/м³.

3.3. Безпосередньо вимірюваними величинами є d, L, t. Діаметр кульки вимірювався мікрометром з індикатором годинникового типу. Ціна поділки – 0, 01 мм. Межі вимірювання 0…10 мм. Шлях L вважався рівним відстані між рисками на посудині і вимірювався стандартною лінійкою з ціною поділки 1мм. Час вимірювався секундоміром з ціною поділки 0, 2 с.

Таблиця вимірюваних величин

Результати вимірювань подаються у вигляді таблиці. При цьому слід мати на увазі таке: при первинних вимірах допускається (і навіть корисно) записувати значення вимірюваної величини у тих одиницях, у яких градуйована шкала приладу (мм, мГ, мкА, кількість поділок шкали приладу і т.д.).

Це робиться тому, що у разі помилки при переході до основних одиниць, можна було б її знайти і виправити. Якщо ж таких записів немає, то у разі помилки все треба починати з початку.

Приклади:

а) сила F = 12, 1 мГ = 12, 1·10^-3 Г = 0, 118 Н;

б) вимірюється сила струму. Кількість поділок приладу, що відповідає даній силі струму n = 20. Ціна поділки – С =0, 05 А/под. Тоді сила струму

І = n · С =20 под·0, 05 А/под=1 А.

У таблиці, що подається у звіті, значення всіх величин наводяться в одиницях системи SI. При цьому може статися так, що в таблицю треба записувати або дуже великі, або дуже малі числа. У таких випадках треба користуватися записом числа в нормованій формі: а = 1, 23·10^-10 (1, 23 – мантиса, 10^-10 – порядок). Мантиса числа повинна містити одну цифру до коми.

Приклади:

а) сила F = 1520 Н = 1, 52·10³ Н;

б) питома теплоємність с = 4190 Дж/(кг·К) = 4, 19·10³ Дж/(кг·К);

в) момент інерції І = 0, 00312 кг·м² = 3, 12·10^-3 кг·м².

У таблиці наводяться значення лише тих величин, що безпосередньо вимірюються на досліді. Символ величини, порядок числа та одиниця вимірювання записуються у верхівці таблиці. Числові значення величин (мантиси) записуються у колонці таблиці. Кількість цифр після коми у кожному стовпчику таблиці повинна бути однаковою. Крім того слід пам’ятати, що остання цифра будь-якого числа вважається не точною. Отже кількість цифр у результаті виміру слід обирати з урахуванням відносної похибки вимірювань.

Приклади:

а) результат окремого виміру х = 15, 25. Відносна похибка виміру не менше за 5%. Абсолютна похибка виміру: s _х = 15, 25·0, 05=0, 76. Отже результат виміру слід обирати з урахуванням відносної похибки виміру х =15, 2;

б) отримані такі середні значення для моменту інерції системи, що відповідають різному розподілу маси системи відносно осі обертання:

J ₁ =0, 0024 кг·м²

J ₂ =0, 0030 кг·м²

J ₃ =0, 0068 кг·м²

J ₄ =0, 0075 кг·м²

J ₅ =0, 0120 кг·м²

Можливі два варіанти оформлення цих результатів у вигляді таблиці.

аб

У варіанті б) множник 10³ вказує на те, що в колонку записане число у тисячу разів більше за дійсне. Варіант а) більш природний, тому рекомендуємо користуватися саме ним.

5. Розрахунок шуканих величин

Розрахунок шуканих величин проводиться за робочими формулами. При цьому слід додержуватись правил наближених обчислень (див. глава І, розділ 1).

Порядок обчислення абсолютної та відносної похибки для прямих вимірів наведено у главі І, розділ 2.

Покажемо, як обчислюються похибки для величин, які є результатом непрямих вимірів. При непрямих вимірах порядок знаходження похибок досліду такий:

а) користуючись робочою формулою для визначення шуканої величини, а також виразом

, (1.1)

одержують формулу для підрахунку відносної похибки досліду;

б) підставляючи у робочу формулу середні значення вимірюваних величин, знаходимо середнє значення шуканої величини < у >;

в) визначаємо абсолютну похибку шуканої величини:

; (1.2)

г) кінцевий результат подаємо у вигляді:

. (1.3)

Як приклад, розглянемо підрахунок похибок у роботі №1.1.

Робоча формула для визначення моменту інерції системи має вигляд:

. (1.4)

У досліді вимірюються величини: – висота, на яку опускається тягарець, – час, за який це відбувається, – радіус вала, на який намотана нитка.

Отже, ми можемо вважати, що шукана величина J є функцією трьох змінних. .

Знаходимо частинну похідну (при цьому всі інші величини, що входять у робочу формулу (1.4), вважають сталими):

.

Знаходимо відношення цієї похідної до самої функції:

.

Помножуємо одержану величину на стандартну похибку величини R та підносимо одержаний результат до квадрату:

.

Це і буде перший доданок суми у формулі (1.1). Величини у дужках – відносна похибка вимірювання радіуса вала.

Аналогічно знаходимо другий доданок суми для часу t:

.

Для визначення третього доданку для висоти h знаходимо похідну:

.

Знаходимо відношення цієї похідної до самої функції:

.

Помножуємо одержану величину на стандартну похибку вимірювання висоти () та підносимо до квадрату:

.

В результаті таких дій одержуємо формулу для визначення відносної похибки досліду:

.

Аналізуючи вираз, що знаходиться під радикалом, можна зробити висновок про внесок кожного вимірювання у загальну похибку досліду.

Декілька зауважень щодо визначення похибок досліду.

1. До визначення похибок слід приступати тоді, коли робота виконана, тобто зроблені всі необхідні виміри, оброблені аналітично та графічно, знайдено середнє значення шуканої величини і немає ніяких підстав вважати одержаний результат невірним.

2. Якщо дослід проводиться декілька разів, то для визначення похибок обирається той дослід, у якому абсолютні похибки для вимірюваних величин – найбільші.

3. При визначенні відносної похибки слід її не занижувати, а завищувати, виходячи з тих міркувань, що коли нас задовольнятиме знайдена таким шляхом похибка, то тим більше нас задовольнятиме реальна похибка, яка буде меншою від неї. Звичайно для лабораторних вимірювань відносна похибка досліду не повинна перевищувати 10%.