Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Описати суть трансформації координат методом Гельмерта

Трансформацію координат можна виконати, якщо відомі координати пунктів в обох системах або параметри (“ключі”) переходу. Існує декілька способів розв’язку задачі для кожного з яких необхідна мінімальна кількість вихідних пунктів. Розв'язок буде найбільш достовірним якщо таких пунктів буде більше, що дозволить виконати трансформацію за методом найменших квадратів і оцінити точність отриманих результатів. Трансформація може бути виконана наступними способами:

1. Перетворення методом Гельмерта, при цьому ні кути, ні довжини сторін не деформуються

2. Афінне перетворення, можуть деформуватися і кути і лінії.

В першому випадку перетворення відбуваються зі збереженням масштабу.

Ми розглянемо перетворення двовимірних координат, тому що в сфері землеустрою це завдання виникає найчастіше.

Рис. 6.1.

Два різних набори планових геодезичних координат містяться у векторах 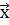та 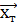. Двовимірне перетворення подібності Гельмерта описується формулою:

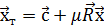(6.1)

де μ – масштабний множник;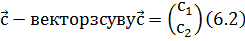

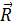– матриця повороту 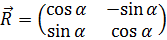(6.3)

Рівняння (6.1) в поєднанні з формулами (6.2) і (6.3) є двовимірним перетворенням Гельмерта з чотирма параметрами, зокрема двома компонентами зсуву с₁ та с₂, масштабним множником μ, а також кутом повороту 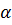. Підстановка рівняння (6.2) і (6.3) у вираз (6.1) дає формули для розрахунку координат точок:

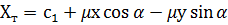
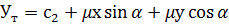(6.4)

Якщо параметри перетворення 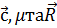відомі то за їх допомогою рівняння (6.4) координати з системи 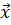можна перетворити в систему 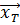. У випадку якщо параметри не відомі, то їх можна визначити використовуючи координати двох спільних точок, застосовуючи допоміжні невідомі:

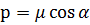
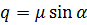(6.5)

Можна записати лінійне рівняння відносно невідомих:

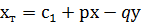
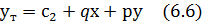
Розглянувши систему цих рівнянь можна зробити висновок, що достатньо мати координати двох точок для розв'язку системи:

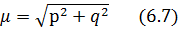
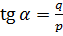(6.8)

Для визначення значень невідомих параметрів достатньо мати координати трьох точок в початковій і кінцевій системі координат, або ж параметри переходу.

Формули Гельмерта використовують в тих випадках, коли локальна мережа при трансформації координат її пунктів в іншу систему координат зберегла свої початкові форму і розміри. Це дуже важливо в тих випадках, коли існують юридичні документи на земельну ділянку (державний акт).