
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Камеральні роботи при обробці результатів вимірювань мережі тріангуляції
|
|
При камеральних роботах дотримуються наступної послідовності:
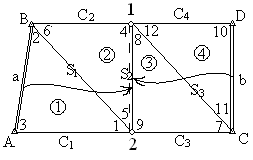
Рисунок. 2.1.
Як видно з рис. 2.1., в мережі виміряно 2 базиси: a i b та всі 3 кути в кожному трикутнику. Під час складання схеми мережі тріангуляції обов’язково нумерують трикутники і кути. 1-й трикутник починають з того трикутника, в якому заміряний базис, а далі - рахують по-порядку. Кути в трикутнику доцільно нумерувати за загальноприйнятою схемою. Всі сторони трикутника мають свою назву та сторони 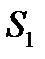 ,
, 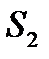 ,
, 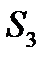 називають зв’язуючими сторонами, тому що вони є спільними для двох сусідніх трикутників.
називають зв’язуючими сторонами, тому що вони є спільними для двох сусідніх трикутників.
Сторони 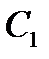 ,
, 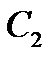 ,
, 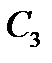 ,
, 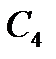 називають проміжними тому, що вони не є спільними з іншими трикутниками.
називають проміжними тому, що вони не є спільними з іншими трикутниками.
Нумерують кути в трикутника за наступним правилом:
1-й кут – проти виміряного базису а;
2-й – проти проміжної сторони;
3-й – проти зв’язуючої сторони 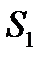 ;
;
Переходять до нумерації кутів у другому трикутнику:
4-й кут – проти 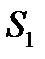 ;
;
5-й – проти проміжної сторони 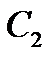 ;
;
6-й – проти зв’язуючої сторони 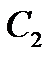 ;
;
Аналогічно в третьому трикутнику:
7-й кут – проти 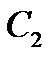 ;
;
8-й – проти проміжної сторони 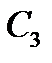 ;
;
9-й – проти 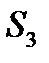 ;
;
В четвертому трикутнику:
кут 10 проти 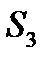 ;
;
11-й – проти проміжної сторони 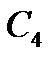 ;
;
12-й – проти базису b.
Така нумерація кутів дозволяє майже автоматично складати базисне рівняння, яке має наступний вигляд:
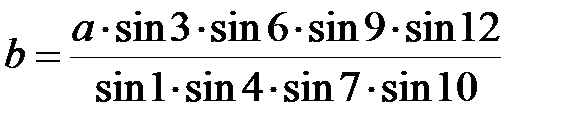
Складання базисного рівняння:
Із першого трикутника згідно теореми синусів:
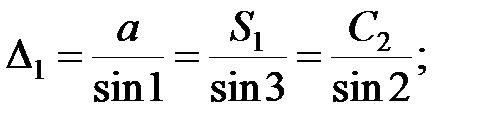
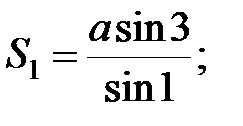
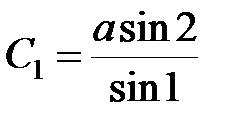 ;
;
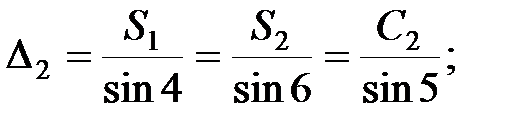
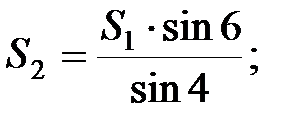
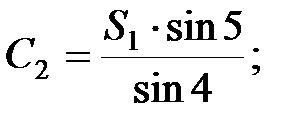
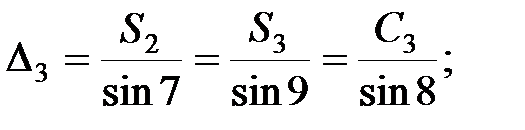
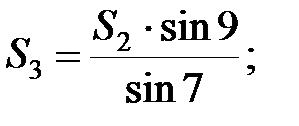
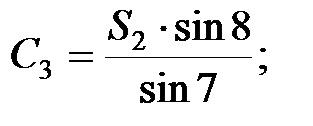
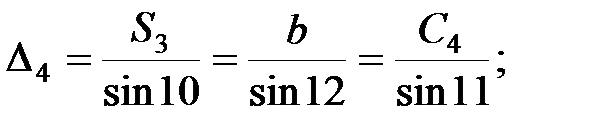
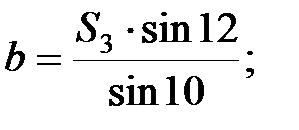
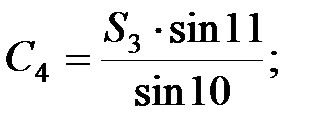
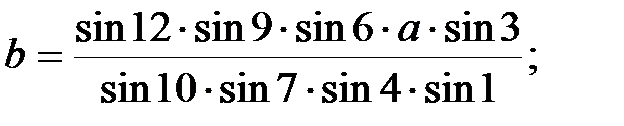
В мережі тріангуляції виникає стільки умов фігур скільки є трикутників. Оскільки в трикутнику вимірюються всі кути, то нев’язка визначається за формулою:
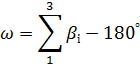
Поправка в виміряні кути вводиться порівну:
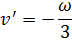
Гранична похибка нев’язки в трикутнику:
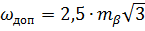
де  - СКП вимірювання горизонтального кута
- СКП вимірювання горизонтального кута
Вільний член базисної умови обчислюється за формулою:
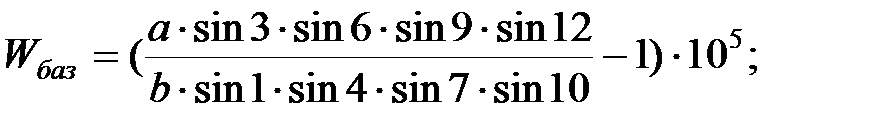
Допустимий вільний член базисного рівняння обчислюється за формулою:
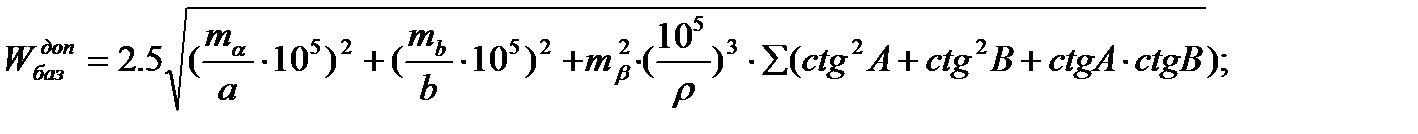
де 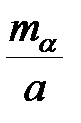 ,
, 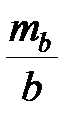 - відносні СКП вимірювання базисів
- відносні СКП вимірювання базисів
Якщо величина вільного члена базисного рівняння менше або рівне допустимої величини, то обчислюють величину вторинної поправки за формулою:
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
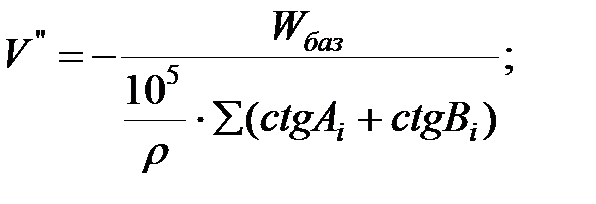
Вторинну поправку додають тільки до зв’язуючих кутів, при чому до кутів, які знаходяться в чисельнику базисного рівняння додають вторинну поправку з тим знаком, який отримали за формулою, а кути, які знаходяться в знаменнику базисного рівняння її додають з оберненим знаком. Слід пам’ятати, що поправки заокруглюють до 0, 1́. Вторинна поправка вводиться з метою, щоб знайти теоретичне місце точки в якій перетинаються промені трикутника і не порушується теоретична умова.
Після цього за урівняними кутами обчислюють довжини сторін трикутників. Контролем обчислень являються рівності вирахуваного і виміряного значення базиса b.
Маючи урівняні кути і довжини ліній, обчислюємо прямокутні координати точок за формулами Юнга (рис.2.2.) або методом теодолітних ходів. 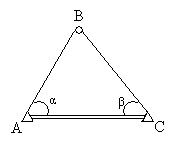
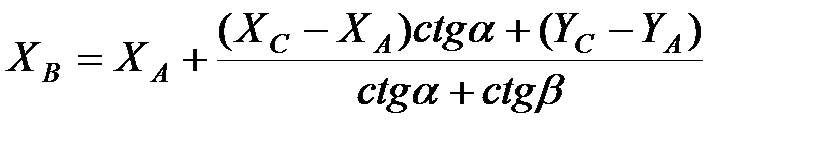
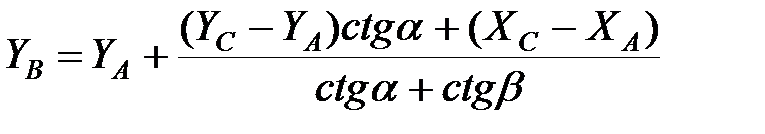
Рисунок 2.2.
Контроль:
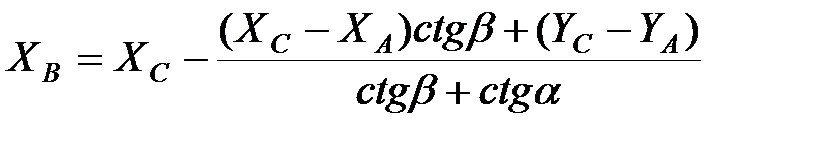
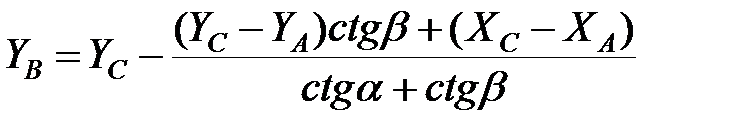
2.3. Виконати урівнювання мережі тріангуляції спрощеним методом 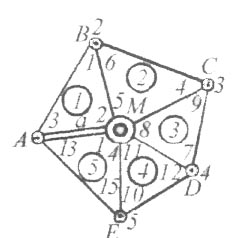
Вихідні дані:
| 1=77°06, 9' | 2=66°47, 0' |
| 3=36°06, 1' | 4=39°28, 6' |
| 5=93°17, 1' | 6=47°14, 3' |
| 7=40°44, 0' | 8=63°50, 5' |
| 9=75°25, 5' | 10=74°36, 8' |
| 11=61°49, 3' | 12=43°33, 9' |
| 13=41°42, 2' | 14=74°16, 0' |
| 15=64°01, 8' | а =129, 93 м |
| α МА=27°21, 4' | |
| Xм=2000, 00 | Yм=3600, 00 |
Рисунок.2.3.Схема мережі тріангуляції
mβ =1", а відстань базиса виміряна з точністю: 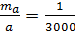
Таблиця 2.1 - Рішення трикутників мережі тріангуляції
| № трик. | № кута | Виміряні кути | Поправки | Виправлені кути | Синуси кутів | Сторони | |
| V' | V'' | ||||||
| 77°06, 9' | +3, 87 | 77°6'57, 87`` | 0, 974829791 | 129, 93 | |||
| 66°47, 0' | 66°47' | 0, 919020707 | 122, 492 | ||||
| 36°06, 1' | -3, 87 | 36°6'2, 13`` | 0, 589204701 | 78, 532 | |||
| ∑ | 180˚ 0, 0' | 180˚ 00' | |||||
| W1 | 0˚ 0, 0' | -3, 87 | |||||
| 39°28, 6 | +2, 89`` | 39°28`38, 87`` | 0, 635774668 | 78, 532 | |||
| 93°17, 1' | 93°17, 1`` | 0, 998356852 | 123, 318 | ||||
| 47°14, 3' | +0, 1 | -2, 89`` | 47°14'15, 11`` | 0, 734174762 | 90, 686 | ||
| ∑ | 179°59`54`` | 180˚ 00' | |||||
| W2 | 0˚ 0'06`/3 | -2, 89`` | |||||
| 40°44, 0' | +4, 35`` | 40°44'4, 35`` | 0, 652555338 | 90, 686 | |||
| 63°50, 5' | 63°50'30`` | 0, 897579204 | 124, 738 | ||||
| 75°25, 5' | -4, 35`` | 75°25'25, 65`` | 0, 967813757 | 134, 498 | |||
| ∑ | 180˚ 0, 0' | 180˚ 0, 0' | |||||
| W3 | 0˚ 0` | -4, 35`` | |||||
| 74°36, 8' | +4, 67`` | 74°36'2, 67`` | 0, 964163182 | 134, 498 | |||
| 61°49, 3' | 61°49'18`` | 0, 881482086 | 122, 965 | ||||
| 43°33, 9' | -4, 67`` | 43°33'49, 33`` | 0, 689160638 | 96, 136 | |||
| ∑ | 180˚ 0, 0' | 180˚ 00' | |||||
| W4 | 0˚ 0, 0' | -4, 67`` | |||||
| 41°42, 2' | +3, 85`` | 41°42'15, 85`` | 0, 665287726 | 96, 134 | |||
| 74°16, 0' | 74°16, 0' | 0, 962534154 | 139, 090 | ||||
| 64°01, 8' | -3, 85`` | 64°01'44, 15`` | 0, 89901528 | 129, 927 | |||
| ∑ | 180˚ 00' | 180˚ 00' | |||||
| W5 | 0˚ 0, 0' | -3, 85`` |
|
|
