Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Обчислення вільного члена базисного рівняння
|
|
Вільний член базисного рівняння обчислюється за формулою:
Wбаз=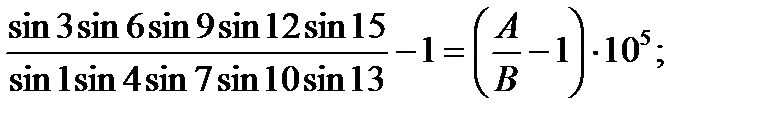 
де А — добуток чисельника базисного рівняння;
В —добуток знаменника базисного рівняння;
W — різниця, яку називають вільним членом базисного рівняння
Обчислення вільного члена базисного рівняння мережі тріангуляції доцільно виконувати в таблиці 2.2.
| Чисельник | Знаменник | ||||||||
| № трик | Випр. Кути | Синуси | сtgАі | сtg2Аі | № трик | Випр. кути | Синуси | сtgВі | сtg2Ві |
| 36°06, 1' | 0, 58921986 | 1, 371 | 1, 88 | 77°06, 9' | 0, 974819607 | 0, 229 | 0, 052 | ||
| 47°14, 3' | 0, 734204025 | 0, 924 | 0, 855 | 39°28, 6 | 0, 635763928 | 1, 214 | 1, 474 | ||
| 75°25, 5' | 0, 967819064 | 0, 260 | 0, 067 | 40°44, 0' | 0, 652539358 | 1, 161 | 1, 348 | ||
| 43°33, 9' | 0, 689177043 | 1, 051 | 1, 105 | 74°36, 8' | 0, 964157175 | 0, 275 | 0, 076 | ||
| 64°01, 8' | 0, 899023453 | 0, 487 | 0, 237 | 41°42, 2' | 0, 665273791 | 1, 122 | 1, 259 | ||
| ∑ | А=0, 259412042 | 4, 193 | 4, 144 | В=0, 259403061 | 4, 001 | 4, 209 |
Таблиця 2.2. - Обчислення вільного члена базисного рівняння
Оскільки в подальшому користуються вільним членом базисного рівняння, як цілим числом, то щоб обчислити це число застосовують формулу:
Wбаз=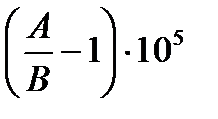 
Wбаз=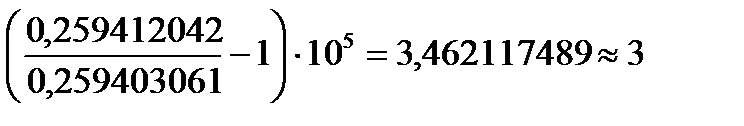 
Після цього обчислюють допустимий вільний член базисного рівняння за формулою:
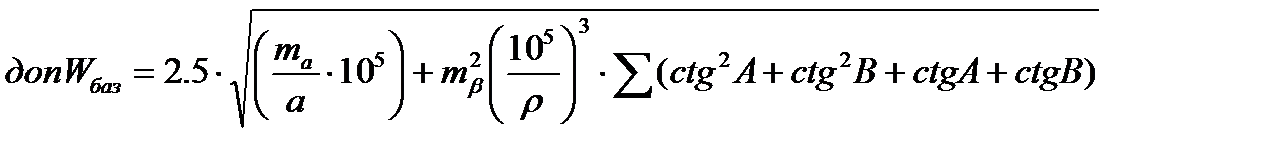
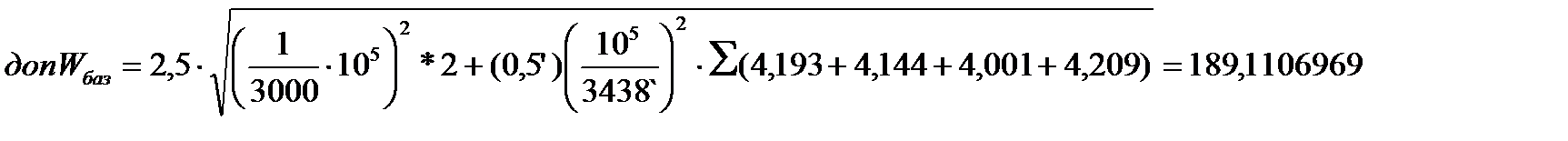
Отже Wбаз<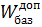 
, тому:
V2 =-3, 87``
V3 =-2, 89``
V4 =-4, 35``
V5 =-4, 67``
V=-3, 85``
Вторинна поправка вноситься у виміряні куті, причому в кути, які знаходяться в чисельнику базисного рівняння з тим же знаком, який отримали за формулою, а в кути, які знаходяться в знаменнику - з протилежним знаком. Після внесення первинних і вторинних поправок у кути отримано виправлені кути. Маючи зрівноважені значення виміряних кутів, можна вирахувати за теоремою синусів довжини сторін мережі трикутників тріангуляції. Після обчислення сторін приступають до обчислення прямокутних координат точок даної мережі.
|
|