
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Розділ 4. Енергія електростатичного поля
|
|
§6. Енергія електростатичного поля
6.1. Енергія точкових зарядів
Розглянемо систему з двох точкових зарядів. Знайдемо алгебраїчну суму елементарних робіт сил F1 i F2, з якими взаємодіють заряди. Нехай в системі відліку К за час ∆ t заряди здійснили переміщення 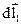 і
і 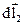 , тоді робота цих сил чисельно дорівнює
, тоді робота цих сил чисельно дорівнює
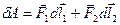 .
.
Враховуючи те, що сила 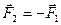 згідно з третім законом Ньютона, вираз для роботи можемо переписати у вигляді:
згідно з третім законом Ньютона, вираз для роботи можемо переписати у вигляді:
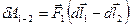 .
.
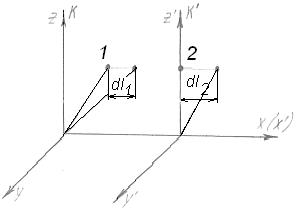 Величина в дужках – переміщення заряду 1 відносно заряду 2 в системі К’, яка жорстко зв’язана з зарядом 2 і переміщується з ним поступально по відношенню до даної системи К.
Величина в дужках – переміщення заряду 1 відносно заряду 2 в системі К’, яка жорстко зв’язана з зарядом 2 і переміщується з ним поступально по відношенню до даної системи К.
Переміщення 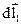 заряду 1 в системі К може бути представлене як переміщення
заряду 1 в системі К може бути представлене як переміщення 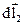 системи К’.
системи К’.
Тоді
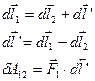
Рис.6.1
З даного виразу бачимо, що сума елементарних робіт в довільній системі відліку К завжди дорівнює елементарній роботі, яку здійснює сила, яка дії на один заряд в системі відліку, де інший заряд знаходиться в стані спокою. Тобто, робота δ А 12 не залежить від вибору К -ої системи відліку.
Сила F1, яка діє на заряд 1 з боку заряду 2 є консервативною і тому робота даної сили по переміщенню на dl1 може бути представлена як зменшення потенціальної енергії заряду 1 в полі заряду 2, або як зменшення потенціальної енергії взаємодії розглядуваної пари зарядів. Тобто, 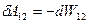 . Потенціальна енергія W12 залежить лише від відстані між зарядами.
. Потенціальна енергія W12 залежить лише від відстані між зарядами.
Перейдемо до системи з трьох зарядів. Роботу, яку здійснюють всі сили взаємодії при переміщенні всіх зарядів можна представити як суму елементарних робіт всіх трьох пар взаємодій.
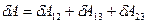 .
.
Але для кожної пари взаємодій 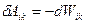 . І тому елементарна робота δ А буде визначатися як:
. І тому елементарна робота δ А буде визначатися як:
 ,
,
де W – повна енергія взаємодії системи зарядів. Кожен доданок залежить від відстані між відповідними зарядами і тому потенціальна енергія взаємодії є функцією конфігурації системи зарядів.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
Подібні міркування характерні для системи з будь-яким числом зарядів.
Отже кожній конфігурації довільної системи зарядів має своє значення енергії і робота всіх сил взаємодії при зміні конфігурації буде чисельно дорівнювати зменшенню потенціальної енергії.
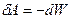 . (6.1)
. (6.1)
Знайдемо вираз для потенціальної енергії W. Для цього розглянемо систему з трьох точкових зарядів.
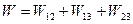 .
.
Перетворимо цю суму наступним чином: представимо кожний доданок Wik у вигляді:
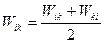 (оскільки Wik=Wki).
(оскільки Wik=Wki).
Тоді повна енергія взаємодії перепишеться у вигляді:
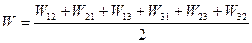 .
.
Згрупуємо члени з однаковими першими індексами:
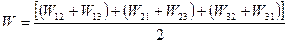 .
.
Кожна сума в круглих дужках – це енергія Wi взаємодії і -го заряду з двома іншими зарядами. Тому останній вираз можемо записати як суму
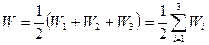 .
.
Узагальнення на систему із довільного числа зарядів очевидне, бо ясно, що при проведенні розрахунків і міркувань вираз не залежить від числа зарядів. Тому енергія взаємодії системи зарядів в загальному випадку:
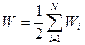 . (6.2)
. (6.2)
Враховуючи, що з означення потенціалу потенціальна енергія чисельно дорівнює добутку заряду на потенціал поля, в якому він знаходиться
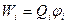 ,
,
де Qi – і -ий заряд системи, φ і – потенціал, створений в місці знаходження і -го заряду всіма іншими зарядами системи. Підставимо цей вираз в формулу (6.2) і отримаємо кінцевий вираз для енергії взаємодії системи точкових зарядів.
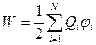 . (6.3)
. (6.3)
Якщо заряди розподілені неперервно, то розкладаючи систему зарядів на сукупність елементарних зарядів 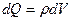 і переходячи від сумування до інтегрування у (6.3) отримаємо, що
і переходячи від сумування до інтегрування у (6.3) отримаємо, що
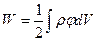 , (6.4)
, (6.4)
де φ – потенціал, створений всіма зарядами системи в елементі об’ємом dV. Аналогічний вираз можна записати при розподілі зарядів по поверхні:
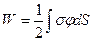 .
.
Можна помилково вважати, що рівняння (6.4) – це лише видозмінений вираз (6.3), який відповідає заміні представлення про точкові заряди представленням про неперервний розподіл зарядів. Насправді, ці вирази відрізняються за змістом. Виникнення розбіжності полягає в різному змісті потенціалу φ.
Нехай, система складається з двох кульок, які мають заряди Q1 i Q2. Відстань між кульками набагато більша, ніж розміри самих кульок, тому заряди Q1 i Q2 можна вважати точковими. Знайдемо енергію системи за допомогою обох формул. Тоді
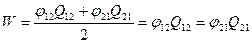 ,
,
де φ 12 – потенціал, створений другим зарядом, в місці знаходження першого. Аналогічний зміст має потенціал φ 21.
Згідно формули (6.4) ми повинні розбити заряд на нескінченно малі заряди величиною ρ dV і кожен з елементів помножити на потенціал, створений не лише іншими кульками, а й елементами даної кульки і, таким чином, результат буде інший.
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.
Для новых пользователей первый месяц бесплатно. Зарегистрироваться в сервисе
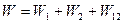 ,
,
де W1 – енергія взаємодії елементів заряду першої кульки, W2 – енергія взаємодії елементів заряду першої кульки, W12 – енергія взаємодії елементів заряду першої кульки з елементами заряду другої кульки.
Енергії W1, W2 називаються власними енергіями зарядів Q1 і Q2 відповідно, W12 – енергія взаємодії зарядів Q1 і Q2.
Таким чином, розрахунок енергії за формулою (6.3) дає лише величину W12, а за формулою (6.4) маємо повну енергію взаємодії (разом з власними енергіями зарядів).
Використовуючи формулу (6.4) можна одержати енергію зарядженого провідника і конденсатора.
6.2. Енергія усамітненого зарядженого провідника
Нехай провідник має заряд Q і потенціал φ, оскільки значення потенціалу в усіх точках, де знаходиться заряд однаковий, то його можна винести за знак інтегралу і тоді під інтегралом залишиться лише величина заряду на провіднику (див. формулу (4)). І враховуючи, що 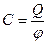
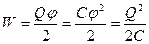 . (6.6)
. (6.6)
6.3. Енергія зарядженого конденсатора
Нехай Q і φ – заряд і потенціал позитивно зарядженої обкладки конденсатора. Згідно (6.4) потенціальну енергію можна розбити на дві частини для двох обкладок:
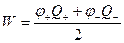 .
.
Так як Q+ = - Q- , то
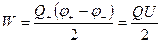 ,
,
U=∆ φ – різниця потенціалів на обкладках конденсатора.
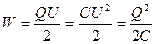 . (6.7)
. (6.7)
Ці формули визначають повну енергію взаємодії.
Формули (6.6) і (6.7) також справедливі при наявності діелектрика.
6.5. Енергія електростатичного поля
Формула (6.4) визначає електричну енергію будь-якої системи через заряд і потенціал, повну енергію можна також виразити через напруженість електричного поля.
Розглянемо плоский конденсатор, не враховуючи змін поля біля країв пластин (тобто нехтуючи крайовим ефектом). Енергія такого конденсатора визначається формулою (6.7).
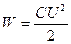 .
.
Підставимо сюди вираз для ємності плоского конденсатора 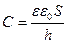 :
:
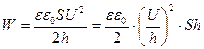 .
.
Оскільки відношення 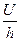 є напруженістю електричного поля, а добуток
є напруженістю електричного поля, а добуток  – об’єм між простору між обкладками конденсатора, остаточно маємо:
– об’єм між простору між обкладками конденсатора, остаточно маємо:
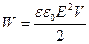 . (6.8)
. (6.8)
Формула справедлива для однорідного поля, який заповнює об’єм V.
Якщо діелектрик ізотропний, враховуючи, що D=ε ε 0E можна також записати
 . (6.9)
. (6.9)
Підінтегральний вираз має зміст енергії поля, яке знаходиться в об’ємі dV, що приводить до ідеї про локалізацію енергії в самому полі. З останніх двох формул слідує, що електрична енергія розподілена в просторі з деякою об’ємною густиною енергії ω.
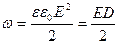 . (6.10)
. (6.10)
Остання формула справедлива лише для ізотропного діелектрика, для якого виконується співвідношення між поляризованістю і напруженістю зовнішнього поля
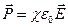 .
.
Питання для самоконтролю
1. Як визначається енергія точкових зарядів?
2. Як визначається енергія заряжених провідника та конденсатора?
3. Як визначається енергія електростатичного поля?
|
|
