Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
⚡️ Для новых пользователей первый месяц бесплатно. А далее 290 руб/мес, это в 3 раза дешевле аналогов. За эту цену доступен весь функционал: напоминание о визитах, чаевые, предоплаты, общение с клиентами, переносы записей и так далее.
✅ Уйма гибких настроек, которые помогут вам зарабатывать больше и забыть про чувство «что-то мне нужно было сделать».
Сомневаетесь? нажмите на текст, запустите чат-бота и убедитесь во всем сами!
Розділ 1. Електростатичне поле у вакуумі
|
|
Електростатичне поле
1.1. Електростатика. Електричний заряд та його властивості
Електростатика – розділ електродинаміки, який вивчає взаємодію нерухомих електричних зарядів. Така взаємодія здійснюється через електростатичне поле.
Електричний заряд – це фізична величина, яка визначає інтенсивність електромагнітних взаємодій. Всі елементарні частинки характеризуються масою та електричним зарядом. Сила електромагнітних взаємодій набагато більша їх гравітаційної взаємодії. Значення сили електромагнітної взаємодії частинок визначається їх електричними зарядами.
Загалом в природі відомо чотири фундаментальні типи взаємодій:
- сильна;
- електромагнітна;
- слабка;
- гравітаційна.
Кожен вид взаємодії пов’язаний з певною характеристикою частинки. Так, гравітаційна залежить від маси частинки, а електромагнітна – від її електричного заряду.
Фундаментальні властивості електричного заряду:
1. Існує в двох видах – негативний (електрон) і позитивний (протон).
2. В будь-якій електрично-ізольованій системі алгебраїчна сума зарядів не змінюється. Ця властивість виражає закон збереження електричного заряду.
.
3. Електричний заряд є релятивістсько інваріантний (його величина не залежить від системи відліку, не залежить від того, рухається він чи знаходиться в стані спокою).
Для спрощення математичних розрахунків, прийнято вважати заряд не дискретним. Тоді його можна замінити піктивним безперервним розподілом. При переході до неперервного розподілу вводиться поняття густини заряду.
Виділяють лінійну (λ, τ), поверхневу (σ) та об’ємну (ρ) густину зарядів:
;
;
.
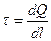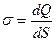Закон збереження зарядів:
Електричні заряди не створюються і не зникають, а передаються від одного тіла до іншого або перерозподіляються всередині даного тіла.
Дробових зарядів в вільному стані не існує.
1.2. Закон Кулона
Основним законом електростатики є закон Кулона (1785 р.). Цей закон показує взаємодію двох нерухомих точкових зарядів або заряджених тіл, розміри яких малі порівняно з відстанями між ними.
Взаємодію заряджених тіл Кулон вивчав за допомогою крутильних вагів. Він виміряв силу взаємодії двох заряджених кульок в залежності від величини зарядів на них та від відстані між ними. При цьому Кулон виходив з того, що дотику до зарядженої металічної кульки такої ж самої незарядженої кульки заряд розподіляється між обома кульками порівну.
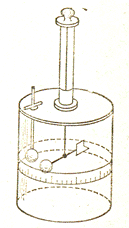В результаті своїх дослідів Кулон прийшов до висновку, що: сила взаємодії двох нерухомих точкових зарядів пропорційна величині кожного з зарядів і обернено пропорційна квадрату відстані між ними.
Напрямок сили співпадає з прямою, що сполучає заряди. В умовах цієї взаємодії однойменні заряди відштовхуються, а різнойменні притягуються (рис.1.1).
,
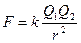k – коефіцієнт пропорційності (залежить від вибору системи одиниць)
,
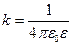Рис.1.1
де ε – діелектрична проникливість середовища, ε 0 – електростатична стала (ε 0=8, 85·10-12 Ф/м).
В системі СІ одиниця електричного заряду – Кл („кулон”).
1 Кл – електричний заряд, який проходить за 1с через поперечний переріз провідника при струмі 1А.
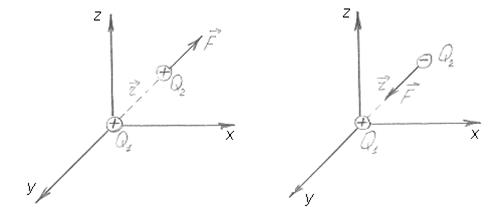
Рис.1.2
Таким чином, електростатичне поле – особливий вид матерії, пов’язаний з електричними зарядами і яка передає дії зарядів з одного зарядів з одного на другий. Електричне поле не виникає при взаємодії зарядів. Будь-який заряд завжди має електричне поле. Якщо заряд нерухомий, то поле називається електростатичним. Воно не змінюється в часі і створюється лише електричними зарядами.
Електричне поле має специфічні фізичні властивості. На електричні заряди цього поля діють сили, пропорційні цим зарядам. Якщо потрібно виявити електричне поле, то в місце знаходження заряду вносять інший заряд. Для визначення властивостей поля використовують пробний одиничний позитивний заряд Qпр, нехтуючи його власним полем. На Qпр діє сила
.
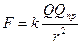1.3. Напруженість електричного поля
Якщо в ту саму точку поля вносити різні заряди, то на них будуть діяти різні сили, але відношення сил до величини заряду буде зберігатися сталим для цієї точки поля:
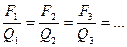
Для різних точок поля можна скласти аналогічні співвідношення.
Відношення сили до величини пробного заряду називається напруженістю електричного поля. Напруженість – силова характеристики електричного поля; відношення сили до величини пробного заряду.
,
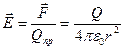r – відстань від заряду Q, який створює поле до точки поля, де визначається напруженість.
Напруженість показує яка сила діяла б на одиничний позитивний (пробний) заряд, вміщений в дану точку поля. Е – векторна величина; за напрям беруть напрям сили, з якою заряд Q діє на дану точку.
Лінії, дотичні до яких в кожній точці збігаються з вектором напруженості в даній точці поля називаються лініями напруженості, або силовими лініями. Силові лінії ніколи не можуть бути замкнені самі на себе – вони завжди мають початок і кінець або йдуть у нескінченність. Вони направлені від позитивного заряду до негативного (виходять з позитивного заряду і входять в негативний). Лінії напруженості ніколи не перетинаються.
Рис.1.3
Електричне поле, у всіх точках якого напруженість однакова за величиною і напрямком називається однорідним (тобто заряд рівномірно розподілений по площині). Прикладом однорідного поля може бути поле плоского конденсатора на деякій відстані від країв пластин конденсатора.
Принцип суперпозиції полів (накладання електричних полів).
Результуюча сила, що діє на заряд Q з боку інших зарядів Q1 > 0 і Q2< 0 буде дорівнювати геометричній сумі сил F1 і F2 з боку зарядів Q1 і Q2.
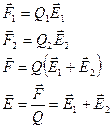
Якщо поле створене двома зарядами, напруженість визначається за теоремою косинусів:
.
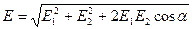Рис.1.4
В загальному випадку: якщо в певній точці поля різні заряджені частинки створюють поля з напруженостями Е1, Е2, Е3... Еn, то результуюча напруженість поля в точці:
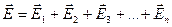
1.4. Потенціал електричного поля
Потенціал – енергетична характеристика електричного поля, що показує яку роботу треба затратити, щоб перемістити заряд в дану точку поля, або перенести його з даної точку поля у нескінченність. Потенціал характеризує потенціальну енергію яку мав би позитивний одиничний заряд, вміщений в дану точку поля.
Робота по переміщенню не залежить від форми шляху, а залежить лише від розміщення початкової і кінцевої точок траєкторії. Робота по переміщенню заряду, яка виконується в електричному колі по замкненому контуру дорівнює нулю.
.
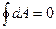При переміщенні зарядів змінюється їх взаємне розміщення і тому робота електричних сил дорівнює зміні потенціальної енергії заряду, що переміщується.
.
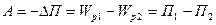Потенціальна енергія заряду в електричному полі визначається за формулою:
.
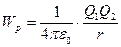Таким чином, потенціал φ
.
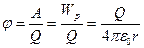Формула справедлива, якщо φ → 0 при r→ 
.
1.5. Зв’язок між напруженістю і потенціалом
Напруженість і потенціал є різними характеристиками однієї точки поля.
Розглянемо роботу електричних сил в електричному полі при переміщенні електричного заряду з точки 1 в точку 2.
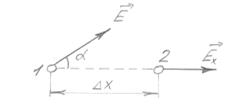A= QEx∆ x;
A=Q (φ 1 –φ 2)= - Q∆ φ.
Прирівнявши обидва вирази для роботи, дістанемо:
QEx∆ x= - Q∆ φ,
Рис.1.5
.
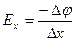Аналогічно,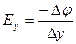 
,
.
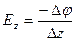Таким чином, Е= - gradφ.
Напруженість в будь-якій точці поля дорівнює швидкості зміни потенціалу в цій точці поля, взятій з протилежним знаком. Знак „мінус” показує, що вектор напруженості направлений в бік спадання потенціалу, тобто вектори напруженості і потенціалу протилежно направлені.
1.6. Еквіпотенціальні поверхні
Уявна поверхня, всі точки якої мають однаковий потенціал називаються еквіпотенціальними поверхнями. Їх рівнянні мають вигляд:
φ (x, y, z)=const.
При переміщенні по еквіпотенціальній поверхні на dl потенціал φ не змінюється (dφ =0). Тоді дотична до поверхні складова вектора напруженості дорівнює нулю. Отже, вектор напруженості в кожній точці направлений по нормалі до еквіпотенціальної поверхні, яка проходить через дану точку. Звідси, лінії напруженості в кожній точці ортогональні до еквіпотенціальної поверхні.
Еквіпотенціальну поверхню можна провести через будь-яку точку поля, тоді таких поверхонь може бути безліч. Проводять такі поверхні таким чином, щоб різниця потенціалів для двох сусідніх поверхонь була всюди одна і та ж сама. В такому випадку, по густині еквіпотенціальних поверхонь можна судити про величину напруженості поля. Чим густіше розташовані еквіпотенціальні поверхні, тим швидше змінюється потенціал при переміщенні вздовж нормалі до поверхні, відповідно, тим більше в даному місці 
і Е.
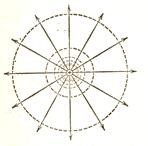Для однорідного поля еквіпотенціальні поверхні представляють собою систему рівновіддалених одна від одної площин, перпендикулярних до напрямку поля.
Для точкового заряду еквіпотенціальні поверхні можна представити у вигляді, показаному на рис.1.5.
Рис.1.6
1.7. Електричний диполь
Електричним диполем називається система двох однакових за величиною різнойменних точкових зарядів +q і –q, відстань l між якими значно менша відстані до тих точок, в яких визначається поле системи. Пряма, яка проходить через обидва заряди називається віссю диполя; l – плече диполя.
Поле диполя має осьову симетрію. Якщо відстань між зарядами не змінюється, то такий диполь називається жорстким. Якщо довжина плеча диполя l мала порівняно з відстанню r до точки спостереження, то такий диполь називається точковим.
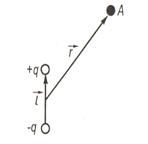Основною характеристикою електричного диполя є його електричний дипольний момент р – вектор, який чисельно дорівнює добуткові заряду на плече і направлений від негативного заряду до позитивного.
.
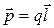Рис.1.7
1.8. Електричний диполь в однорідному зовнішньому електричному полі
Розглянемо дію зовнішнього електричного поля на диполь.
Якщо поле однорідне, то сили, які діють на негативний і позитивний заряди диполя є однаковими за значенням і протилежними за напрямом, тобто утворюють пару сил(рис1.8). Відповідно їх рівнодія дорівнює нулю.
Дія пари сил характеризується моментом пари:
M= qElsinα,
α – кут між вектором l і напруженістю поля Е.
, тоді
М=plsinα.
Або у векторній формі
.
Рис.1.8
Отже, в однорідному електричному полі на диполь діє пара сил, яка намагається повернути диполь так, щоб кут між векторами р і Е зменшився і диполь встановився в напрямку поля.
Існують два положення рівноваги диполя:
- диполь паралельний електричному полю (стійка рівновага);
- диполь антипаралельний йому (нестійка рівновага).
Енергія диполя в однорідному електричному полі напруженістю Е:
.
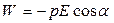1.8. Електричний диполь в неоднорідному зовнішньому електричному полі
Якщо поле неоднорідне, то сили F1 і F2 за значенням є різними і їхня рівнодія не дорівнює нулю.
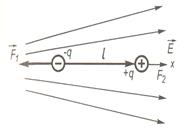Знайдемо рівнодійну силу. Вважатимемо, що диполь розміщений вздовж однієї з силових ліній (рис 1.9). Тоді 
.
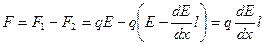Таким чином, в неоднорідному електричному полі на диполь крім моменту пари сил, діє ще сила в напрямі зростання напруженості поля, яка прагне втягнути диполь в область сильнішого поля.
Рис. 1.9
|
|