Тема 1. Системы счисления

Системой счисления называется совокупность приемов наименования и записи чисел.

Все системы счисления делятся на два больших класса – непозиционные и позиционные.

В непозиционной системе счисления значения символов не зависят от положения в числе. Для образования таких систем используют, в основном, операции сложения и вычитания. Например, система с одним символом-палочкой встречалась у многих народов. Для изображения числа в этой системе нужно записать определенное множество палочек, равное данному числу. Эта система не эффективна, т.к. запись числа получается длинной. Другим примером непозиционной системы счисления является римская система.

Основными числами в римской системе счисления являются 1, 5, 10, 50, 100, 500, 1000, которые обозначаются следующими знаками: I, V, X, L, C, D, M, а другие получаются путем сложения и вычитания базисных: если цифра слева меньше, чем цифра справа, то левая цифра вычитается из правой.

Так, например, число 146 в римской системе счисления имеет вид CXLVI (C – 100, XL – 40, VI – 6), здесь «сорок» получается посредством вычитания из «пятидесяти» числа «десять», «шесть» - посредством сложения «пяти» и «единицы».

Примеры:

XXVII = 10+10+5+1+1=27;

MMMD = 1000+1000+1000+500=3500;

MCMXCIV = 1000+(1000-100)+(100-10)+(5-1)=1994.

При таком представлении чисел правила сложения для небольших чисел очевидны и просты, однако если возникает необходимость выполнять операции сложения над большими числами или операции умножения и деления, то римская система счисления оказывается неудобной.

В позиционной системе счисления значение каждого символа изменяется от ее положения (или позиции) в числе. Привычной для всех является десятичная система счисления.

Количество различных символов, применяемых в позиционной системе счисления, называется ее основанием.

В вычислительной технике широко используются двоичная, восьмеричная и шестнадцатеричная системы счисления. Обозначим через p основание системы счисления, тогда при p= 2 {0, 1}; p= 8 {0, 1, 2, 3, 4, 5, 6, 7}; p= 16 {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E}. Наряду с этими системами счисления используются и другие системы счисления, в которых используется свой набор символов. Так, например, в системе счисления по основанию 11 существуют символы от 0 до А, по основанию 13 – от 0 до С и т.д.

В позиционной системе с некоторым основанием р используются р различных между собой символов от 0 до р-1. Так последовательность символов

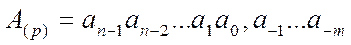
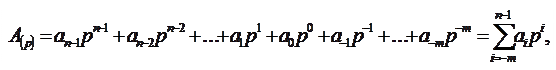в р -ичной системе означает число:

где a_i -цифры системы счисления, n и m – число целых и дробных разрядов числа.

Примеры:

37541, 234 ₁₀=3´ 10⁴ + 7´ 10³ + 5´ 10² + 4´ 10¹ + 1´ 10⁰ + 2´ 10^-1 + 3´ 10^-2 + 4´ 10^-3

123, 5₇ = 1´ 7² + 2´ 7¹ + 3´ 7⁰ + 5´ 7^-1

§1. Перевод чисел из системы счисления с основанием p в десятичную систему счисления

Пусть исходное число Аp содержит m разрядов. Для того чтобы целое число Аp перевести в десятичную систему счисления, достаточно цифру старшего разряда числа Аp умножить на основание системы счисления p, возведенное в степеньсоответствующую номеру позиции цифры данного разряда за минусом единицы (m-1). К полученному произведению прибавить цифру следующего (более младшего) разряда числа Аp, умноженную на основание p, возведенное в степень m-2. И так до тех пор, пока не будет прибавлена младшая цифра исходного числа Аp возведенное в степень 0.

Пример №1. Перевести число Х=9А07, С8₁₆ в десятичную систему счисления, пользуясь правилами десятичной арифметики.

Для перевода воспользуемся формулой (1.1) и запишем число 9А07, С8₁₆ в виде:

9А07, С8₁₆ = 9´ 16³ + 10´ 16² + 0´ 16¹ + 7´ 16⁰ + 12´ 16^-1 + 8 ´ 16^-2

Выполним все необходимые действия в десятичной системе и получим ответ:

Х = 36864+2560+0+7+0, 75+0, 03125

Ответ: 9А07, С8₁₆ = 39431, 78125₁₀

Пример №2. Перевести число Х=AF4₁₆ в десятичную систему счисления.

Для перевода запишем число AF4₁₆ в виде:

Х = А ´ 16²+ F ´ 16¹+4 ´ 16⁰;

Х = 10 ´ 16²+15´ 16¹+4´ 16⁰ =2560+240+4=2804

Ответ: AF4₁₆ = 2804₁₀

Пример №3. Перевести число Х=1101, 101₂ в десятичную систему счисления.

1101, 101₂ = 1´ 2³ + 1´ 2² + 0´ 2¹ + 1´ 2⁰ + 1´ 2^-1 + 0´ 2^-2 + 1´ 2^-3=13, 625

Ответ: 1101, 101₂ = 13, 625₁₀

Пример №4. Перевести число Х=325₆ в десятичную систему счисления.

325₆ = 3´ 6² + 2´ 6¹ + 5´ 6⁰ =125

Ответ: 325₆= 125₁₀

Пример №5. Перевести число Х=275₈ в десятичную систему счисления.

Х = 2 ´ 8 ²+ 7 ´ 8¹+5 ´ 8⁰ = 189

Ответ: 275₈ = 189₁₀

§2. Перевод десятичных чисел в систему счисления по основанию p