Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Линейная структура алгоритма

Линейная структурапредставляется просто последовательностью записью операторов (рис.3).

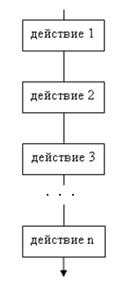
Рис.3

Алгоритмы с линейной структурой являются простейшими и используются, как правило, для реализации простых вычислений.

Рассмотрим линейную структуру на следующем примере.

Пример №1. Вычислить площадь параллелограмма.

Последовательность действий при решении данной задачи описана блок-схемой алгоритма, представленной на рис.4.

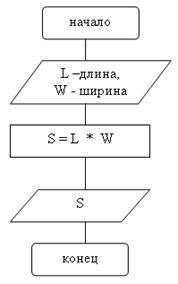
Рис.4.

В данном алгоритме выполняется последовательность действий: сначала вводятся исходные данные L и W, а затем выполняется вычисление площади параллелограмма S = L*W и последним действием является вывод выходных данных S.

§4.2. Структура алгоритма «цикл с предусловием»

В этой структуре «действие» будет повторяться до тех пор, пока будет выполняться условие (по ветке «+»). Поэтому в «действии» должно изменяться значение переменных, от которых зависит «условие», в противном случае произойдет зацикливание (рис.5). Проверка «условия» производится до начала выполнения «действия» и может случиться так, что «действие» не будет выполнено ни разу.

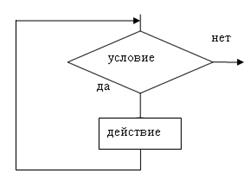
Рис.5

Рассмотрим структуру алгоритма «цикл с предусловием» на следующем примере.

Пример №2. Протабулировать функцию y = sin x, при изменении аргумента x от х₁ до х₂ с постоянным шагом h_x.

Последовательность действий при решении данной задачи описана блок-схемой алгоритма, представленной на рис.6.

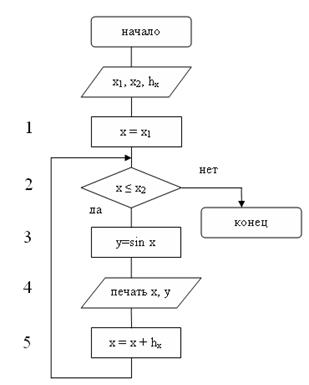
Рис.6

Пояснения к блок-схеме (рис.6):

1. Аргументу x функции y присваивается начальное значение диапазона изменения аргумента;

2. Проверяется условие окончания цикла (х≤ х₂). Действия 1 – 4 выполняются до тех пор, пока не будет достигнут конец диапазона изменения аргумента х;

3. Вычисляется значение функции у;

4. Вывод на экран аргумента х и функции у;

5. Аргументу функции х прибавляется его приращение h_x.

§4.3. Структура алгоритма «цикл с постусловием»

Цикл с постусловием (рис.7) всегда выполняется хотя бы один раз, «действие» перестает выполняться, как только будет выполнено «условие» (по ветке «+»).

Рис.7

Рассмотрим структуру алгоритма «цикл с постусловием» на следующем примере.

Пример №3.

Вычислить значения функции y = ab⁵+ a⁷b, при всех возможных сочетаниях аргументов a и b, если, а изменяется от a₁ до a₂ с постоянным шагом h_а, а b изменяется от b₁ до b₂ с постоянным шагом h_b.

Последовательность действий при решении данной задачи описана блок-схемой алгоритма, представленной на рис.8.

Алгоритм решения этой задачи заключается в следующем: необходимо при каждом значении аргумента функции b вычислить все значения а.

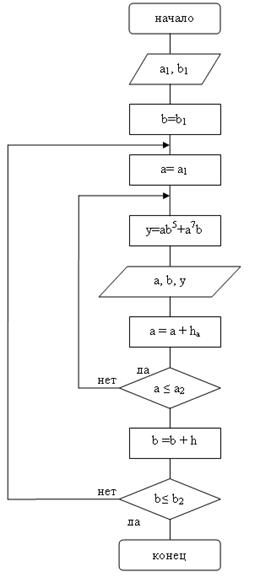
Рис.8

Пояснения к блок-схеме (рис.8):

1. Аргументам а и b функции y присваиваются начальные значения диапазона изменения аргументов a₁ и b₁;

2. Вычисляется значение функции у;

3. Вывод на экран аргументов a, b и функции у;

4. Аргументам функции a и b прибавляются их приращения h_a и h_b;

5. Проверяются условия окончания циклов a≤ a₂ и b≤ b₂. Действия выполняются до тех пор, пока не будут достигнуты конечные значения диапазонов изменений аргументов a и b.