Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Формулировка задачи как вариационной задачи на условный экстремум.

Для этого необходимо рассматривать в качестве уравнения связей уравнение системы (1), а в качестве функционала – функционал (2).

Таким образом, получаем следующую вариационную задачу:

Определить функции x(t) и u(t) доставляющие экстремум функционалу

,

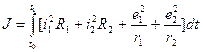при граничных условиях

,

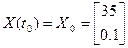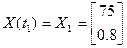
и при дополнительных условиях (уравнениях связи)

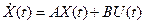
накладываемом на функции x(t), u(t), в классе которых ищется экстремум.

Синтез алгоритма оптимального управления – решение вариационной задачи на условный экстремум.

Составляется функция Лагранжа:

.

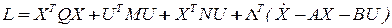Записываются уравнения Эйлера-Лагранжа:

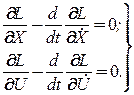(7)

Вычисляются составляющие соотношений (5.6):

;

.

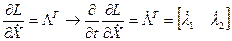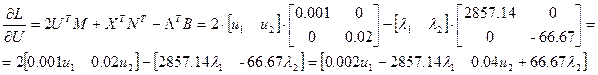
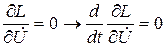Тогда уравнения Эйлера-Лагранжа принимают вид:

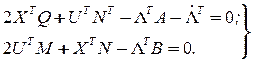(8)

К последним уравнениям добавляется уравнение связи (уравнение объекта) получается следующая система уравнений:

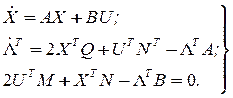(9)

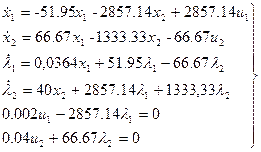(10)

Найдем U:

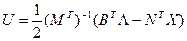
и подставим в первые два уравнения (10):

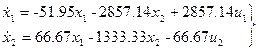(11)

Введем вектор 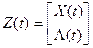. Тогда систему (10) с учетом (11) можно представить в виде:

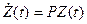(12)

где Р – блочная матрица, имеющая вид:

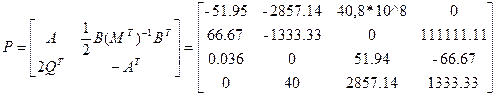(13)

Решение (12) в соответствии с формулой Коши:

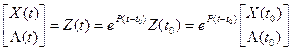(14)

Вычислив 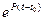, ее можно представить следующим образом:

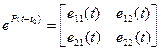(15)

где 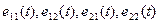- функциональные матрицы размеров .

Тогда из выражений (14), (15):

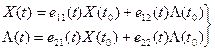(16)

Для определения начального значения множителя Лагранжа запишем следующие соотношения:

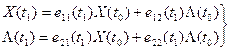(17)

Из первого уравнения (17) можно определить начальное условие множителя Лагранжа:

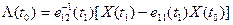
(18)

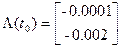
Теперь можно записать из выражений (16):

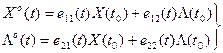(19)

Оптимальное управление определится выражением:

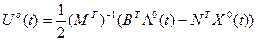
Таким образом найдены соотношения для оптимальной траектории и оптимального управления:
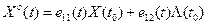
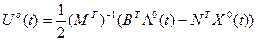