
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Описание объекта управления. Математическая модель объекта получается на основе законов Кирхгофа и имеет вид линейных дифференциальных уравнений
|
|
Математическая модель объекта получается на основе законов Кирхгофа и имеет вид линейных дифференциальных уравнений, векторно-матричный вид которых

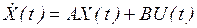 ,
,
где 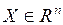
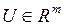
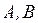 – матрицы чисел размерами
– матрицы чисел размерами 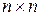 и
и 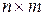 соответственно.
соответственно.
Начальное положение (состояние) объекта: 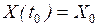 .
.
Конечное положение (состояние) объекта: 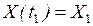 .
.
Уравнения электрической схемы можно получить в виде:
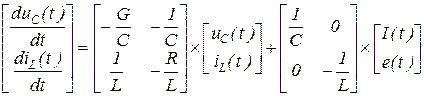 , (1)
, (1) 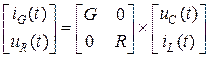 . (2)
. (2)
Эти уравнения записаны в форме Коши.
Введем обозначения:
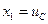
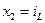 ,.
,.
Тогда выражения (1), (2) можно записать в виде:
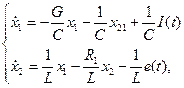
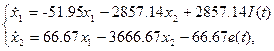 (3)
(3)
Уравнения для выходных переменных
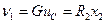
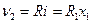 ,. (4)
,. (4)
Объединяя (3) и (4), получаем математическую модель электрической схемы:
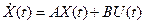 (5)
(5)
Где при  Ф,
Ф, 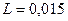 Гн,
Гн, 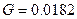 [1/Ом],
[1/Ом],  Ом соответствующие матрицы получают следующие численные значения:
Ом соответствующие матрицы получают следующие численные значения:
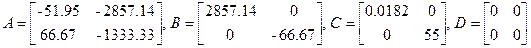 .
.
Начальное положение объекта: 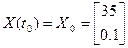
Конечное положение объекта: 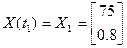
|
|
