
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Описание объекта управления. Математическая модель объекта получается на основе законов Кирхгофа:
|
|
Математическая модель объекта получается на основе законов Кирхгофа: 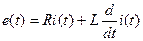
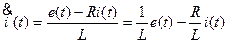
и имеет вид дифференциального уравнения
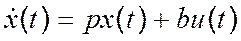 , (1)
, (1)
где x(t)=i(t), u(t)=e(t), p, b – числа, равные p = – R/L, b = 1/L
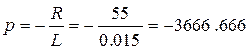
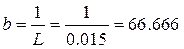
1.2. Конструирование функционала – критерия оптимальности.
Критерий оптимальности – квадратичный функционал

где 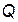 - симметричная, неотрицательно-определенная матрица чисел, размерами
- симметричная, неотрицательно-определенная матрица чисел, размерами 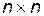 ;
; 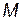 - симметричная, положительно-определенная матрица чисел размерами
- симметричная, положительно-определенная матрица чисел размерами  .
.
В данном случае вместо матриц используются числа, поэтому критерий оптимальности будет иметь другой вид:
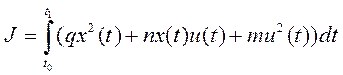 , (2)
, (2)
Это выражение представляет собой суммарную энергию активных потерь в схеме за время t1–t0.
Запишем выражение для активной мощности потерь на сопротивлениях r и R:
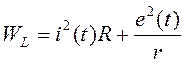 или,
или, 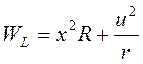
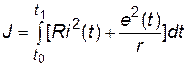
Таким образом, q = R=55, m = 1/r =1/5 =0, 2, n = 0.
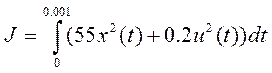
1.3. Формулировка задачи как вариационной задачи на условный экстремум.
Для этого необходимо рассматривать в качестве уравнения связей уравнение системы (1), а в качестве функционала – функционал (2).
Таким образом, получаем следующую вариационную задачу:
Определить функции x(t) и u(t) доставляющие экстремум функционалу
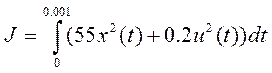 ,
,
при граничных условиях
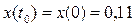 ,
, 
и при дополнительном условии (уравнении связи)
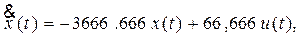
накладываемом на функции x(t), u(t), в классе которых ищется экстремум.
1.4. Синтез оптимального алгоритма управления.
1.4.1. Получение уравнений вариационной задачи.
Введем вспомогательную функцию (функцию Лагранжа)
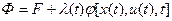 ,
,
где  - пока неизвестная функция, называемая неопределенным множителем Лагранжа.
- пока неизвестная функция, называемая неопределенным множителем Лагранжа.
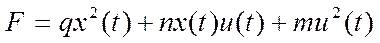
Рассматриваемая задача называется задачей Лагранжа.


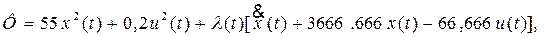
l(t) – неопределенный множитель Лагранжа, Φ – функция Лагранжа.
Запишем уравнения Эйлера для функции  (они называются уравнениями Эйлера – Лагранжа)
(они называются уравнениями Эйлера – Лагранжа)
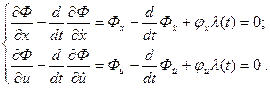
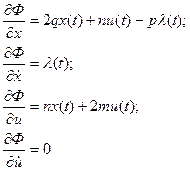
Решим совместно уравнения Эйлера – Лагранжа и уравнение связи. Это система трех уравнений для определения трех неизвестных x (t), u(t), l(t).
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
В итоге получаем систему уравнений
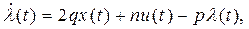
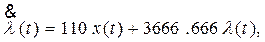 (3)
(3)

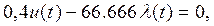 (4)
(4)
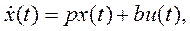
 (5)
(5)
Здесь (3), (4) – уравнения Эйлера – Лагранжа. К этим уравнениям добавлено уравнение объекта (5) (уравнение связи).
1.4.2. Отыскание решения уравнений вариационной задачи.
Уравнения (3) – (5) решаются в следующем порядке:
1) Выразим u(t) из (4):

Затем подставим его в (5).
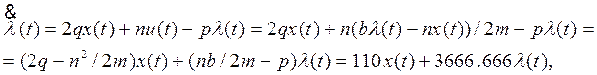
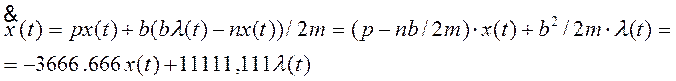
При этом получается система уравнений
 ,
, 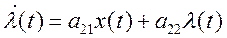 (6)
(6)
с коэффициентами
a11 = p – nb/2m = - 3666.666,
a12 = b2/2m = 11111.111,
a21 = 2q – n2/2m =110,
a22 = nb/2m – p = 3666.666.
Получим систему уравнений:

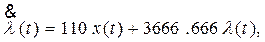
2) Запишем систему (6) в матричной форме
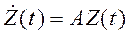 , (7)
, (7)
где
 ,
,
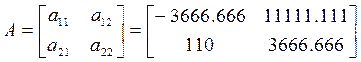 .
.

3) Запишем решение уравнения (7) в соответствии с формулой Коши в виде:
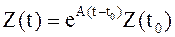 , (8)
, (8)
где
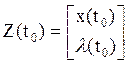 – вектор начальных условий, а матричная экспонента
– вектор начальных условий, а матричная экспонента 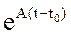 определяется по формуле Лагранжа – Сильвестра
определяется по формуле Лагранжа – Сильвестра
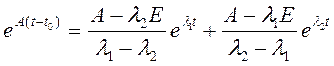 ,
,
где l1, l2 – собственные числа матрицы А. Е - единичная матрица.
Найдем собственные числа матрицы А из условия 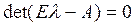 . Получим:
. Получим:
 ,
,
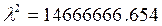 ,
,

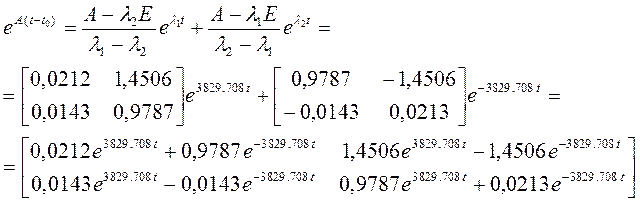
Из системы следует, что для нахождения 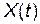 и
и 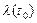 необходимо знать начальные значения
необходимо знать начальные значения 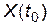 и
и 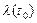 .
.
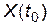 (начальное положение объекта) задано,
(начальное положение объекта) задано, 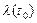 неизвестно.
неизвестно.
Для определения неизвестного начального значения множителя Лагранжа l(t0), входящего в (8) необходимо:
а) запишем (8) для момента времени t1
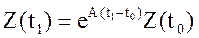
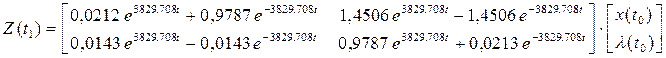
или
 ,
,
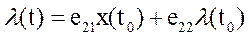 , (9)
, (9)
где e11, е12, е21, е22 – элементы матрицы (числа):
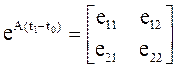
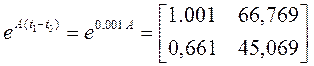
б) определим l(t0) из первого уравнения системы (9)
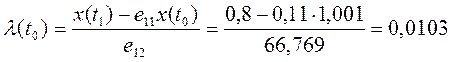
Получили, что 
Решаем уравнение (7):
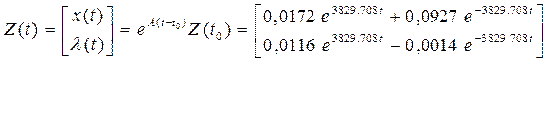
4) Решив уравнение (7), запишем выражения для оптимальной траектории и оптимального управления:
 - оптимальная траектория
- оптимальная траектория
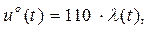
 - оптимальное управление
- оптимальное управление
|
|
