Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Тема 5. Барометрическая формула. Распределение Больцмана.

Барометрическая формула определяет зависимость атмосферного давления воздуха от высоты. Молекулы воздуха находятся, с одной стороны, в потенциальном поле сил тяготения Земли, а, с другой –, в состоянии теплового хаотического движения, что приводит к некоторому стационарному состоянию, при котором давление газа с высотой убывает.

Если атмосферное давление на высоте h равно р (рис. 4), то на высоте h+dh оно равно p+dp, причем при dh > 0 изменение давления dp < 0.

Так как dh настолько мало, что при изменении высоты h в этих пределах плотность воздуха 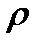можно считать постоянной, то разность давлений:

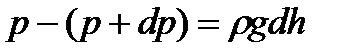, то есть .

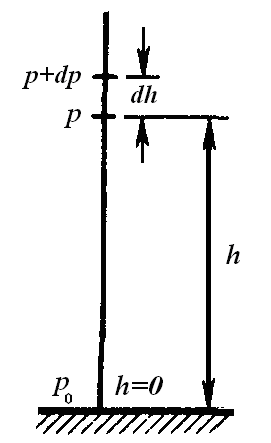
Рис. 4

Выражение для плотности газа 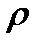можно получить из уравнения состояния идеального газа 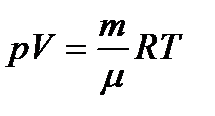, а именно ,

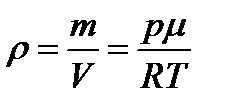где m – масса газа, 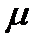– молярная масса газа.

Тогда или .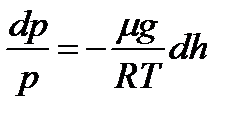

С изменением высоты от 0 до h давление изменяется от р ₀ до р (рис. 4). Поэтому, интегрируя в этих пределах предыдущее уравнение, получим:

, то есть ,

откуда

.

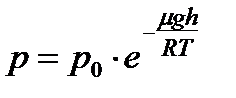Это выражение называется барометрической формулой, где р ₀ – давление на нулевом уровне отсчета высоты h, то есть на уровне, где принято h = 0.

Барометрическую формулу можно преобразовать в зависимость концентрации молекул воздуха n от высоты h, если воспользоваться уравнением состояния идеального газа p=nkT:

,

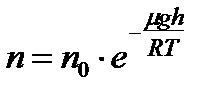где n – концентрация молекул воздуха на высоте h,

n ₀ – концентрация молекул воздуха на высоте h= 0.

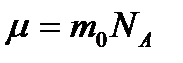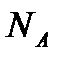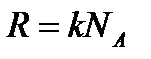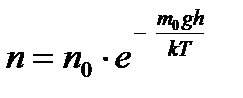Так как (m ₀ – масса одной молекулы, – постоянная Авогадро), a , то или .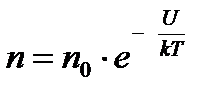

В этой формуле 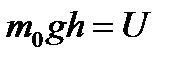, где U – потенциальная энергия молекулы массой m ₀, находящейся в поле сил тяготения Земли на высоте h от уровня, на котором потенциальная энергия молекул воздуха принята равной нулю, а концентрация молекул обозначена как n ₀. Тогда n соответствует концентрации молекул в том месте, где потенциальная энергия молекулы воздуха равна U. Таким образом, получено распределение молекул по потенциальной энергии в силовом поле (распределение Больцмана).