
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Тема 10. Механика жидкости. Уравнение Бернулли
|
|
Гидростатика. Для несжимаемой жидкости ее плотность не зависит от давления. При поперечном сечении S столба жидкости плотностью r ивысотой h давление жидкости р на нижнее основание:
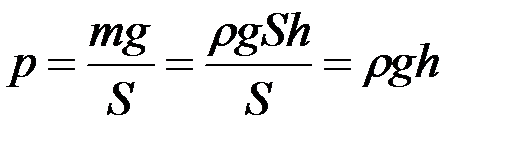 .
.
Давление 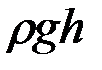 называется гидростатическим давлением.
называется гидростатическим давлением.
Гидродинамика. Графически движение жидкостей изображается с помощью линий тока, которые проводятся так, что касательные к ним совпадают по направлению с вектором скорости жидкости в соответствующих точках пространства (рис. 9). Линии тока проводятся таким образом, чтобы их густота характеризовала величину скорости: густота больше там, где больше скорость течения жидкости, и меньше там, где жидкость течет медленнее.
Часть жидкости, ограниченную линиями тока, называют трубкой тока ( рис. 10 ). Течение жидкости называется установившимся (или стационарным), если форма и расположение линий тока, а также значения скоростей в каждой ее точке со временем не изменяются.
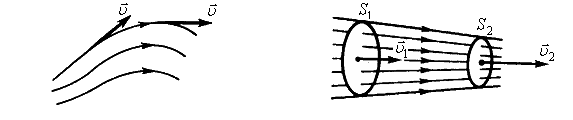
Рис. 9 Рис. 10
Уравнение неразрывности струи для несжимаемой жидкости. Рассмотрим какую-либо трубку тока. Выберем два ее сечения S 1 и S 2 , перпендикулярные направлению скорости (рис. 10).
За время Dt через сечение S 1 проходит объем жидкости 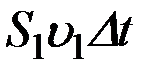 , где
, где 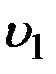 – скорость течения жидкости в месте сечения S 1 , а через сечение S 2 за тоже время Dt пройдет объем жидкости
– скорость течения жидкости в месте сечения S 1 , а через сечение S 2 за тоже время Dt пройдет объем жидкости 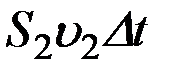 , где
, где  – скорость течения жидкости в месте сечения S 2 . Если жидкость несжимаемая, то через сечение S 2 пройдет такой же объем жидкости, как и через сечение S 1 , т. е.
– скорость течения жидкости в месте сечения S 2 . Если жидкость несжимаемая, то через сечение S 2 пройдет такой же объем жидкости, как и через сечение S 1 , т. е.
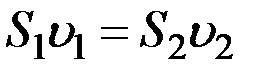 .
.
Так как положения сечений S 1 и S 2 выбраны произвольно, то отсюда следует, что вдоль данной трубки тока 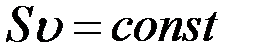 . Это соотношение называется уравнением неразрывности
. Это соотношение называется уравнением неразрывности
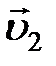
|
| p 2 |
| p 1 |
| h 1 |
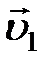
|
| h 2 |
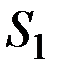
|
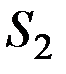
|
Уравнение Бернулли. Бернулли рассмотрел изменения гидродинамических параметров вдоль произвольно выбранной трубки тока стационарно текущей жидкости плотностью r (рис. 11).
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
Рис. 11
В месте сечения трубки тока S 1 скорость течения жидкости 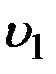 , давление p 1 и высота, на которой это сечение расположено относительно выбранного уровня отсчета, h 1. Аналогично, в месте сечения трубки тока S 2 скорость течения жидкости
, давление p 1 и высота, на которой это сечение расположено относительно выбранного уровня отсчета, h 1. Аналогично, в месте сечения трубки тока S 2 скорость течения жидкости 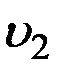 , давление p 2 и высота расположения этого сечения над тем же уровнем отсчета h 2 .
, давление p 2 и высота расположения этого сечения над тем же уровнем отсчета h 2 .
Бернулли установил, что для любых двух сечений одной трубки тока несжимаемой жидкости выполняется равенство:
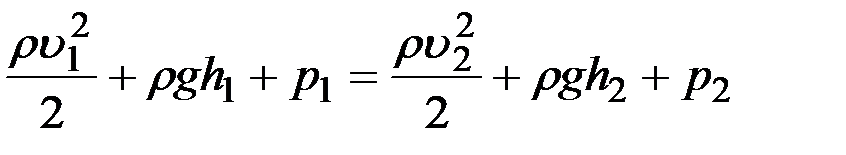 .
.
Так как положения сечений было выбрано произвольно, то для любой трубки тока несжимаемой жидкости гидродинамические параметры жидкости подчиняются следующему уравнению (уравнению Бернулли):
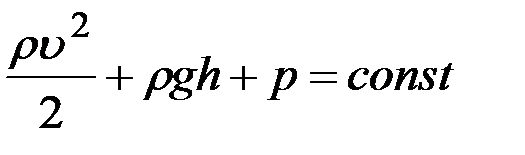 .
.
Для горизонтальной трубки тока (h = const) уравнение Бернулли принимает вид:
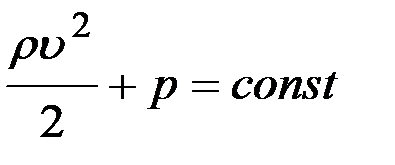 ,
,
где величина 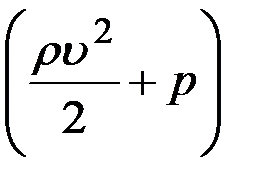 называется полным давлением,
называется полным давлением,
величина р называется статическим давлением,
величина  называется динамическим давлением.
называется динамическим давлением.
Из уравнения Бернулли для горизонтальной трубки тока и уравнения неразрывности струи следует, что при течении жидкости по горизонтальной трубе, имеющей различные сечения, скорость жидкости больше в местах сужения, а статическое давление, наоборот, в местах сужения меньше.
| S2 |
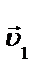
|
| S1 |
| h |
| h2 |
| h1 |
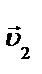
|
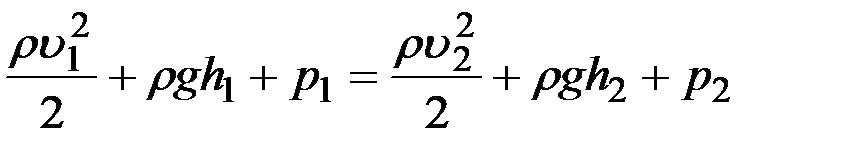 .
.
Так как давления р 1 и р 2 жидкости на уровнях первого и второго сечений равны атмосферному, то р 1 =р 2 , а полученное соотношение примет вид:
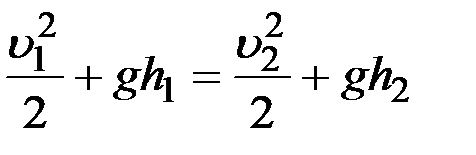 .
.
Из уравнения неразрывности струи следует, что 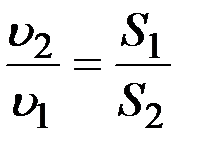 ,
,
где S 1 и S 2 – площади поперечных сечений сосуда и отверстия.
Так как S 1 > > S 2 , то 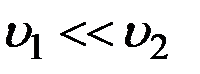 и членом
и членом 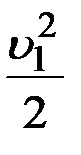 можно пренебречь.
можно пренебречь.
Тогда 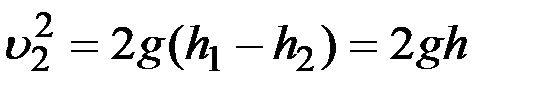 ,
,
откуда  .
.
Это выражение получило название формулы Торричелли, где h – высота свободной поверхности жидкости в сосуде над уровнем отверстия.
Формула Торричелли справедлива только для идеальной жидкости, то есть для жидкости, в которой отсутствует вязкость или внутреннее трение. Только в этом случае скорость истечения жидкости из малого отверстия такая же по величине, как и скорость тела, свободно падающего с высоты h.
|
|
