Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Тема 6. Явления переноса (диффузия, теплопроводность, вязкость).

В неравновесных системах возникают особые необратимые процессы, называемые явлениями переноса, в результате которых происходит пространственный перенос массы, энергии, импульса.

Диффузия обусловлена переносом массы, теплопроводность – переносом энергии, а вязкость – переносом импульса.

Для характеристики необратимых процессов переноса вводятся параметры теплового движения молекул: среднее число соударений молекулы в единицу времени 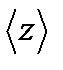и средняя длина свободного пробега молекул .

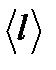Среднее число соударений молекулы за 1 с определяется по формуле:

,

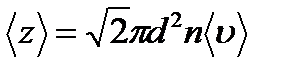где d – эффективный диаметр молекул, т.е. минимальное расстояние, на которое сближаются при столкновении центры двух молекул,

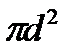– эффективное сечение молекул, 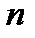– концентрация молекул,

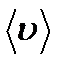– средняя арифметическая скорость молекул.

Средняя длина свободного пробега молекул 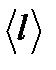, т.е. средний путь, проходимый молекулой между двумя последовательными столкновениями:

.

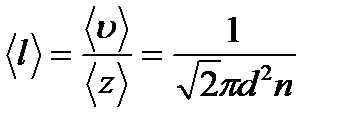При рассмотрении одномерных явлений переноса система отсчета выбирается так, чтобы ось х была ориентирована в направлении переноса.

1. Диффузия. Явление диффузии заключается в том, что происходит самопроизвольное взаимопроникновение и перемешивание частиц двух соприкасающихся газов, жидкостей и даже твердых тел. Диффузия сводится к переносу массы, возникает и продолжается до тех пор, пока на границе соприкосновения двух сред градиент плотности отличен от нуля.

Градиент плотности 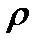вдоль выбранной оси х, перпендикулярной плоскости соприкосновения двух сред, обозначается как 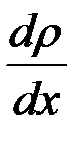и показывает как быстро изменяется величина плотности 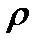от точки к точке вдоль оси х.

Количественно явление диффузии подчиняется закону Фика:

,

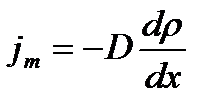где 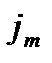– плотность потока массы, то есть величина, определяемая массой газа, диффундирующего через единичную площадку S в единицу времени,

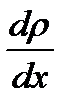– градиент плотности газа в направлении x, перпендикулярном выбранной площадке S,

D – коэффициент диффузии.

Знак минус в приведенной формуле означает, что перенос массы происходит в направлении убывания плотности.

Согласно молекулярно-кинетической теории идеального газа, коэффициент D:

,

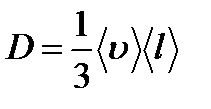где 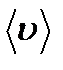– средняя скорость теплового движения молекул,

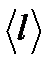– средняя длина свободного пробега молекул.

2. Теплопроводность. Если в одной области газа температура больше, чем в другой, то с течением времени вследствие постоянных столкновений молекул происходит процесс выравнивания средних кинетических энергий молекул, то есть процесс выравнивания температуры. Этот процесс переноса энергии, называемый теплопроводностью, возникает и продолжается до тех пор, пока на границе соприкосновения двух частей газа градиент температуры отличен от нуля.

Градиент температуры Т газа вдоль выбранной оси х, перпендикулярной плоскости соприкосновения двух частей газа, имеющих различную температуру, обозначается как 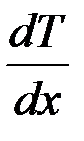и показывает как быстро изменяется температура газа от точки к точке вдоль оси х.

Количественно теплопроводность подчиняется закону Фурье:

,

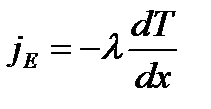где 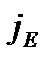– плотность теплового потока – величина, определяемая энергией, переносимой в форме теплоты через единичную площадку S в единицу времени,

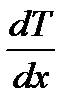– градиент температуры в направлении x, перпендикулярном выбранной площадке S,

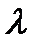– коэффициент теплопроводности.

Знак минус в приведенной формуле означает, что при теплопроводности энергия переносится в направлении убывания температуры.

Согласно молекулярно-кинетической теории идеального газа, коэффициент

теплопроводности 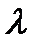определяется следующим образом:

,

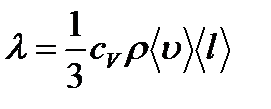где 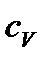– удельная теплоемкость газа при изохорном процессе (количество теплоты, необходимое для изохорного нагревания 1 кг газа на 1 К),

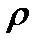– плотность газа,

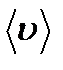– средняя скорость теплового движения молекул,

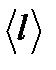– средняя длина свободного пробега молекул.

3. Вязкость. Вязкость это свойство жидкости или газа, обусловленное внутренним трением между соприкасающимися параллельными слоями жидкости или газа, движущимися с различными скоростями. В результате, импульс слоя, движущегося быстрее, уменьшается, а движущегося медленнее – увеличивается, что приводит к торможению слоя, движущегося быстрее, и ускорению слоя, движущегося медленнее. Другими словами, внутреннее трение приводит к переносу импульса от одного движущегося слоя жидкости или газа к другому соприкасающемуся с ним слою.

Количественно сила внутреннего трения между двумя соприкасающимися слоями жидкости или газа подчиняется закону Ньютона:

,

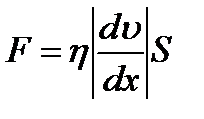где h – коэффициент динамической вязкости,

– градиент скорости, показывающий быстроту изменения скорости течения жидкости или газа от слоя к слою в направлении х, перпендикулярном направлению движения слоев,

S – площадь соприкосновения слоев жидкости или газа, на которые действует сила внутреннего трения F.

Закон Ньютона для внутреннего трения можно представить в виде:

,

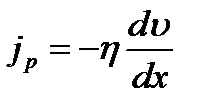где 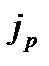– плотность потока импульса – величина, определяемая импульсом, переносимым в единицу времени через единичную площадку S соприкосновения слоев жидкости или газа в направлении оси х, перпендикулярном направлению движения слоев жидкости или газа.

Знак минус в приведенной формуле означает, что импульс переносится от слоя к слою жидкости (газа) в направлении убывания скорости их движения.

Согласно молекулярно-кинетической теории идеального газа, коэффициент

динамической вязкости идеального газа h определяется следующим образом:

,

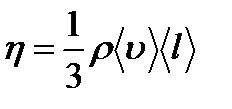где 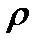– плотность газа,

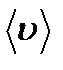– средняя скорость теплового движения молекул,

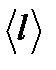– средняя длина свободного пробега молекул.