
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Электрической цепи синусоидального тока. 1. Исследовать электрическое состояние линейной неразветвленной цепи синусоидального тока при различных приемниках.
|
|
Цель работы:
1. Исследовать электрическое состояние линейной неразветвленной цепи синусоидального тока при различных приемниках.
2. Экспериментально проверить условие, при котором наблюдается резонанс напряжений. Определить добротность цепи.
3. По опытным данным построить векторные диаграммы напряжений и тока. Рассчитать параметры отдельных элементов электрической цепи.
Основные теоретические положения
При расчете неразветвленной электрической цепи синусоидального тока с последовательно соединенными приемниками, например катушкой индуктивности и конденсатором, характеризуемых параметрами Rк, L и С (рис.1), исходят из уравнения второго закона Кирхгофа для мгновенных значений напряжений: u = uRк+uL+uC.
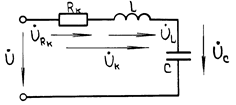
Рис.1
Если к цепи приложено напряжение
u = Um sin (wt + yu) = Umsin wt,
то мгновенный ток становится равным
i = Im sin (wt + yi) = I 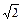 sin (wt + yi),
sin (wt + yi),
где Im и I = 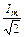 - соответственно амплитудное и действующее значения тока.
- соответственно амплитудное и действующее значения тока.
Расчет в цепях переменного тока производят символическим методом по действующим значениям тока и напряжения.
В комплексной форме
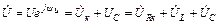 ;
;
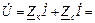 (Rк + jXL)
(Rк + jXL) 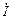 - jXC
- jXC 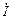 = [ Rк+ j (XL - XC)]
= [ Rк+ j (XL - XC)] 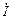 = (Rк + jX)
= (Rк + jX) 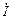 =
=
= Z 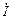 = Ze jj
= Ze jj 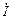 ,
,
где XL = wL = 2 pfL - индуктивное сопротивление катушки;
XC = 1 /wC = 1/ 2 pfC - емкостное сопротивление;
X = XL - XC - реактивное сопротивление цепи;
Z к = Rк + jXL = Zкe jjк - комплексное сопротивление катушки индуктивности;
Z = R + jX = Ze jj - комплексное сопротивление цепи;
Z =  - модуль комплексного сопротивления, представляющий полное сопротивление неразветвленной цепи;
- модуль комплексного сопротивления, представляющий полное сопротивление неразветвленной цепи;
j = yu - yi = arctg (X/ Rк) - угол сдвига фаз между напряжением и током, определяемый из треугольника сопротивлений цепи.
Из предыдущего уравнения комплекс тока равен:
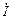 =
= 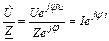 .
.
Модуль комплексного тока I определяет действующее значение тока в цепи: I = 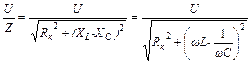 .
.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
В зависимости от соотношения XL и XC полное сопротивление цепи Z может носить активно-индуктивный (XL > XC), активно-емкостный (XL< XC) или чисто активный (XL = XC) характер. Векторные диаграммы напряжений при различных нагрузках приведены на рис.2.
Понятия мгновенной, активной, реактивной, полной мощностей, соотношений между ними описаны в лабораторной работе № 5.
В неразветвленной цепи (рис.1) активная мощность P = UI cos j = URкI = =RкI 2 = Pк выделяется на активном сопротивлении катушки. При взаимной компенсации напряжений UL и UC (рис.2, б) имеет место резонанс напряжений.
Условием резонанса напряжений является равенство реактивных сопротивлений: 2 pf 0 L = 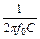 .
.
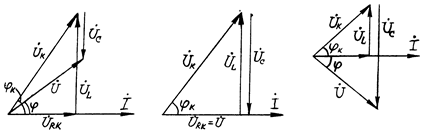
XL > XC; j > 0 XL = XC; j = 0 XL< XC; j < 0
а б в
Рис.2
Из условия резонанса напряжений определяется резонансная частота:
f 0 = 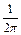
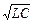 .
.
При резонансе напряжений полное сопротивление цепи Z = Rк, действующее значение тока (I 0 = U/ Rк) достигает наибольшего значения, сдвиг по фазе между током и напряжением отсутствует: j = 0, цепь носит чисто активный характер, из сети потребляется только активная мощность P = UI 0 , она максимальна.
Если R< XL 0 и R< XС 0 , то при резонансе действующие напряжения на реактивных элементах, равные:
UL 0 = XL 0 I 0 = (XL 0 / Rк) U; UC 0 = XC 0 I 0 = (XС 0 / Rк) U,
превышают приложенное напряжение U. Это превышение напряжений (UL 0 = =UC 0 ), по сравнению с U, характеризует добротность цепи q:
q = UL 0 / U = UС 0 / U = XL 0 / Rк = XС 0 / Rк.
Реактивное сопротивление при резонансной частоте называют волновым или характеристическим сопротивлением цепи:
Zв = 2 pf 0 L = 1/ 2 pf 0 C = 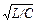 .
.
Добиться резонанса напряжений в цепи, как следует из условия резонанса, можно изменением параметров цепи L, C, частоты f.
Описание установки
Экспериментальное исследование линейной неразветвленной электрической цепи выполняют на установке, электрическая схема которой приведена на рис.3.
Питание цепи осуществляется через понижающий трансформатор. Клем- мы трансформатора через пакетный переключатель подсоединяются к фазе напряжения трехфазной сети.
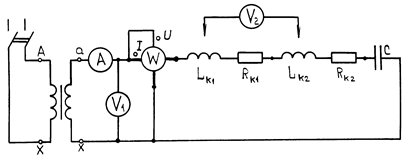
Рис.3
Горизонтальное положение рукоятки пакетного переключателя соответствует выключенному состоянию. Напряжение вторичной обмотки трансформатора подается на исследуемую цепь (клеммы аx). Установка состоит из пакетного переключателя, понижающего лабораторного автотрансформатора, двух индуктивных катушек, добавочного резистора R, батареи конденсаторов. За исключением вольтметра V 1, в установке применены приборы настольного исполнения. Вольтметр V 1предназначен для измерения напряжения на входных клеммах исследуемой цепи. Многопредельный вольтметр V 2 служит для измерения напряжения на катушке индуктивности и конденсатора. Ваттметр и амперметр предназначены для измерения активной мощности и тока.
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.
Для новых пользователей первый месяц бесплатно. Зарегистрироваться в сервисе
Порядок выполнения работы
1. Ознакомиться с приборами и оборудованием экспериментальной установки и записать технические характеристики в отчет.
2. Собрать цепь из двух последовательно соединенных катушек индуктивности и батареи конденсаторов. Изменяя емкость батареи конденсаторов, добиться резонанса напряжений, при котором ток достигает максимального значения и активная мощность P = S = UI. Зафиксировать резонансную мощность.
3. Произвести опыты, изменяя емкость от 0 до Ср (3…4 опыта) и в таких же пределах выше Ср (3…4 опыта). Вблизи резонансной емкости измерения делать чаще. Данные измерений занести в табл. 1.
4. Произвести необходимые вычисления. Учитывая, что параметры катушек не изменялись, достаточно их рассчитать один раз.
При резонансе определить добротность цепи и данные занести в табл.1. Таблица 1
| № Данные наблюдений | Результаты вычислений | ||||||||||||||
| С, мкФ | U, В | I, А А | Р, Вт | Uк, B | Uс, B | S, ВА | Q, ВАр | cosj | Z, Oм | Rк , Ом | Xк, Ом | Xc, Ом | X, Ом | q | |
| 1¸ 9 |
5. Уменьшить индуктивность цепи. Для этого отключить вторую катушку с Rкz, Lкz, замкнув ее перемычкой накоротко. Изменяя емкость батареи конденсаторов, снова найти Ср, при которой в цепи возникает резонанс напряжений. Произвести измерения аналогично п.3, данные занести в табл. 2.
Таблица 2
| № | Данные наблюдений | Вычислено | ||||||||
| С, мкФ | U, В | I, А | Р, Вт | Uк, В | Uc, В | Z | Rк 1 | Xк 1 | q | |
| 1: 9 |
6. По данным табл. 2 рассчитать параметры катушки Xк 1, R к 1, добротность цепи q. Так как параметры катушки не изменяются, достаточно рассчитать их один раз, например при резонансе напряжений. Записать формулу для определения резонансной емкости Cрез. Объяснить изменение Cрез в п.3 и п.5.
7. По данным табл. 1 и 2 для исследуемой цепи построить на одном графике для каждой зависимости Uк, Uc, I от емкости С батареи конденсаторов. По расчетным данным табл. 1 построить зависимости S, cos j на одном графике от величины емкости батареи конденсаторов. Сделать выводы о влиянии частоты питающей сети и емкости на определяемые параметры. Сравнить теоретические кривые и полученные на основании экспериментальных данных.
8. Построить в масштабе по опытным данным табл. 1 векторные диаграммы напряжений и тока для трех состояний цепи: до резонанса, при резонансе и после резонанса.
Указание. При построении векторной диаграммы напряжений (см. рис.2) вектор тока 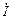 совмещают с действительным направлением оси + I комплексной плоскости. Напряжение на катушке опережает ток на угол jк, определяемый параметрами катушки индуктивности:
совмещают с действительным направлением оси + I комплексной плоскости. Напряжение на катушке опережает ток на угол jк, определяемый параметрами катушки индуктивности:
Zк = 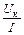 ; Rк =
; Rк = 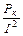 ; Xк =
; Xк = 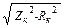 ; jк = arccos
; jк = arccos 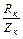 .
.
Для построения вектора 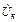 необходимо определить угол jк или составляющие напряжения катушки: активную URк = Rк I, совпадающую с током, и индуктивную ULк = XLк I, опережающую ток на угол p /2. Сдвиг по фазе между током и напряжением на конденсаторе jc = - p /2. Обратить внимание, что при резонансе
необходимо определить угол jк или составляющие напряжения катушки: активную URк = Rк I, совпадающую с током, и индуктивную ULк = XLк I, опережающую ток на угол p /2. Сдвиг по фазе между током и напряжением на конденсаторе jc = - p /2. Обратить внимание, что при резонансе 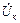 >
> 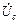 , так как лишь индуктивная составляющая напряжения катушки равна напряжению на конденсаторе: UL = Uc.
, так как лишь индуктивная составляющая напряжения катушки равна напряжению на конденсаторе: UL = Uc.
Вопросы для самоконтроля
1. От каких величин зависит значение угла сдвига фаз между напряжением и током?
2. Что называется индуктивным и емкостным сопротивлениями, от чего они зависят?
3. Каким способом можно измерить величины индуктивности и емкости реактивных приемников?
4. От каких величин зависит полное сопротивление электрической цепи?
5. Как рассчитать действующее значение тока в неразветвленной части цепи с приемниками, характеризуемыми сосредоточенными параметрами R, L и С?
6. Каково условие резонанса напряжений?
7. Как определяется резонансная частота, резонансная емкость?
8. Дать понятие добротности контура.
9. Как рассчитывают активную, реактивную и полную мощность в линейной электрической цепи синусоидального тока?
10. Для последовательной цепи, состоящей из R, L и С при постоянном значении действующего напряжения на зажимах цепи вывести и проанализировать зависимости I, Uк, Uс , S от емкости С и частоты генератора f.
11. Как по известным параметрам R, L, C определить напряжения на отдельных элементах и участках цепи и построить векторные диаграммы напряжений?
Список литературы
1. Электротехника / Под ред. В. Г. Герасимова. – М.: Высшая школа, 1985. –
С. 68-73, 81-86.
2. Касаткин А. С., Немцов М. В. Электротехника. – М.: Энергоатомиздат, 1983. –
С. 57-84, 94-97.
3. Иванов А.А. Электротехника: Лабораторные работы. – Киев: Вища школа, 1976. – С. 60-67.
3. Бессонов Л. А. Теоретические основы электротехники. – М.: Высшая школа,
1984. – С. 76-93, 95-96.
|
|
