Востановительного потенциала

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

Метод электродвижущих сил (ЭДС) широко используется для определения различных физико-химических величин. Применяя его, можно определить произведение растворимости малорастворимых солей, числа переноса, активности и коэффициенты активности электролитов, константы нестойкости комплексных ионов, стандартные электродные потенциалы. Он является основой потенциометрического титрования, применение которого позволяет решить ряд аналитических задач.

Сущность метода ЭДС состоит в измерении электродвижущей силы гальванического элемента. При этом в зависимости от решаемой задачи конструируется тот или иной гальванический элемент.

В случае необходимости определения стандартного потенциала электрода собирается гальваническая цепь из электрода сравнения и индикаторного электрода, на котором протекает интересующая нас реакция. При работе гальванического элемента в условиях близких к равновесию максимальная полезная работа А_mах химической токообразующей реакции равна убыли свободной энергии Гиббса Δ G. В простейшем случае, когда имеет место взаимное превращение только двух веществ, получаем

А_mах = – Δ G = RTln K_а – RTln 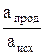, (1)

где К_а – константа равновесия реакции, протекающей в гальваническом элементе; а_прод – начальная активность продукта реакции, а _исх – начальная активность исходного реагента.

Электрическая работа, совершаемая гальваническим элементом за счет протекающей реакции, связана с величиной ЭДС (Е) уравнением

А_mах = nFE = – Δ G, (2)

где n – число электронов, участвующих в химической реакции, F – число Фарадея, Кл/(моль эквивалентов).

Используя уравнения (1) и (2), запишем выражение для ЭДС гальванического элемента:

Е = 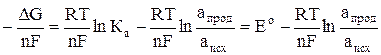, (3)

где Е^о = 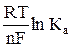– ЭДС элемента в стандартных условиях, то есть при активности веществ, участвующих в реакции равных единице.

Окислительно-восстановительный электрод представляет собой инертный металл (Pt, Au и др.), погруженный в раствор с определенной концентрацией окисленной и восстановленной форм одного и того же вещества. Гальванические элементы, составленные из двух окислительно-восстановительных электродов, являются разновидностью химических цепей.

В качестве примера можно привести гальванический элемент

Pt | Sn⁴⁺, Sn²⁺||Fe³⁺, Fe²⁺| Pt. (4)

Электродные процессы на обоих электродах представляют собой окислительно-восстановительные реакции между ионами

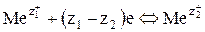, (5)

где z₁⁺, z₁– заряд и величина заряда иона высшей степени окисления, соответственно; z₂⁺, z₂ – заряд и величина заряда иона низшей степени окисления.

ЭДС гальванического элемента Е равна разности между потенциалами более положительного электрода и менее положительного электрода.

Е = 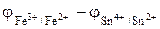. (6)

Значения стандартных потенциалов можно найти в справочниках.

Потенциал окислительно-восстановительных электродов выражается уравнением

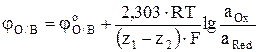, (7)

где a_Ox – активность иона высшей степени окисления, a_Red – активность иона низшей степени окисления.

Поскольку активность i-го иона в растворе a_i равна произведению его концентрации m_i на коэффициент активности g_i, a_i = g_i·m_i то уравнение (7) после преобразования можно привести к виду

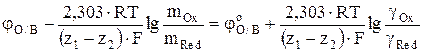, (8)

где m_Ox и g_Ox – моляльная концентрация и коэффициент активности иона высшей степени окисления, соответственно; m_Red и g_Red – моляльная концентрация и коэффициент активности иона низшей степени окисления, соответственно.

По теории сильных электролитов Дебая – Хюккеля для i-го иона:

lg g_i = –Az_i² 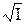, (9)

где I = – ионная сила раствора; A – постоянная; m_i – моляльная концентрация i-го иона; z_i – заряд i-го иона.

Используя уравнение (9), логарифм отношения коэффициентов активности ионов можно представить как

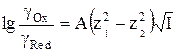. (10)

Тогда уравнение (8) можно записать в виде

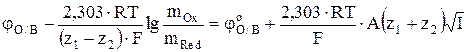. (11)

Левая часть уравнения (11), обозначим ее через φ (I), содержит величины, которые легко определить экспериментально. Для разбавленных растворов можно допустить, что φ (I) является функцией ионной силы раствора. Если построить график в координатах φ (I) – 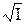, то значение φ (I) при нулевой ионной силе можно определить графически по отрезку, отсекаемому на оси ординат экстраполированной прямой (рис.1). Оно будет равно величине 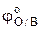стандартного окислительно-восстановительного потенциала электрода.

Рис. 1. Графическое изображение уравнения (11)

ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ

Цель работы – определение стандартной величины потенциала окислительно-восстановительного электрода

Pt | [Fe(CN)₆]^3-, [Fe(CN)₆]^4- . (12)

Порядок выполнения работы

1. Готовят растворы для окислительно-восстановительного электрода, используя соли K₃Fe(CN)₆ и K₄Fe(CN)₆. Концентрацию каждой соли в растворе изменяют в интервале от 0, 01 до 0, 001 моль/дм³ с таким шагом, чтобы получилось не менее шести растворов. В готовом растворе определенной концентрации содержание K₃Fe(CN)₆ и K₄Fe(CN)₆ должно быть одинаковым. При приготовлении растворов учесть взаимное разбавление.

2. Составляют гальваническую цепь (см. рис.2) из окислительно-восстановительного электрода и электрода сравнения (например, хлорсеребряного)

Ag | AgCl, КС1_нас || [Fe(CN)₆]^3–, [Fe(CN)₆]^4– | Pt. (13)

ЭДС цепи равна разности между потенциалом окислительно-восстановительного электрода и потенциалом электрода сравнения.

3. Измеряют ЭДС цепи компенсационным методом, заменяя растворы для окислительно-восстановительного электрода от меньших концентраций к большим.

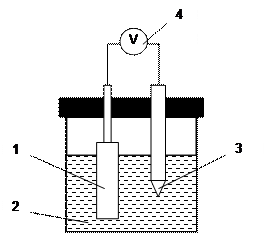Рис.2. Схема установки для измерения ЭДС гальванической цепи.

1 – окислительно-восстановительный электрод; 2 – электролит; 3 – электрод сравнения;

4 – высокоомный потенциометр

Обработка результатов опыта

1. На основании измеренных величин ЭДС, используя уравнение

Е = 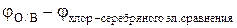, (14)

вычисляют потенциал окислительно-восстановительного электрода относительно водородного электрода сравнения.

2. Рассчитывают ионную силу раствора I.

3. Строят график в координатах φ (I) – .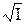

4. Линейной экстраполяцией на ось φ (I) определяют величину φ °_о/в.

5. По уравнению φ °_О/В = 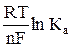рассчитывают константу равновесия токообразующей реакции, протекающей в гальваническом элементе.

Результаты измерений и вычислений сводят в таблицу.

Таблица 1. Экспериментальные и рассчитанные результаты.

Концентрация K3Fe(CN)6, моль/дм3	Концентрация K4Fe(CN)6, моль/дм3	Е, В	φ О/В , В	I		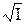φ °О/В, В	Ка

Сравнивают экспериментальное значение φ °_О/В с табличным.

По результатам работы делают выводы и вычисляют абсолютную и относительную ошибки.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Какие электроды сравнения вы знаете?

2. Напишите уравнения потенциалов для электродов первого и второго рода.

3. Что такое электродный потенциал?

4. Привести примеры гальванических цепей.

5. Вывести уравнение связи между изменением потенциала Гиббса реакции и ЭДС гальванического элемента.

6. Как рассчитать константу равновесия реакции, используя метод ЭДС?

7. Какой реакции соответствует константа равновесия К_а в работе?

8. Как рассчитать ионную силу раствора электролита?

9. Какие типы электродов были использованы в работе?

10. Написать схему электрохимической цепи используемой в работе.

11. Написать реакции электродных равновесий на электродах.

12. Написать уравнения Нернста для потенциалов электродов.

13. Зависимость константы равновесия реакции от температуры.

14. Зависит ли ионная сила раствора от температуры.

15. Размерности величин в уравнениях.