Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сызықтық алгебралық теңдеулер жүйесі. Матрицаның рангі

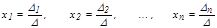А матрицасының рангі деп осы матрицаның нө лге тең емес минорларының ең ү лкен ретін айтады жә не оны 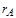, 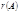немесе 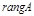деп белгілейді. 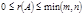болады, мұ ндағ ы 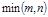- m жә не n сандарының кішісі.

2-ә діс. Элементар тү рлендіру ә дісі. Матрицаны элементар тү рлендіру деп:

1. матрицаның екі жолын (бағ анын) ауыстыру;

2. матрицаның жолын (бағ анын) нө лге тең емес санғ а кө бейту;

3. бір жол (бағ ан) элементтеріне басқ а жолдың (бағ анның) сә йкес қ андай да бір санғ а кө бейтілген элементтерін қ осу амалдарын айтады.

Элементар тү рлендіру арқ ылы алынғ ан матрицаны бастапқ ы матрицағ а эквивалентті матрица дейді жә не орталарына ~ белгісі қ ойылады. Матрицаның рангін табу ү шін элементар тү рлендіруді пайдаланып, матрицаны сатылы тү рге келтіреміз.

Теорема. Матрицаны элементар тү рлендіргеннен оның рангі ө згермейді.

Кері матрица. Егер 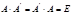шарты орындалса, онда 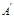матрицасын 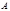матрицасына кері матрица дейді жә не оны 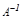тү рінде белгілейді. Мұ ндағ ы 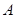, , 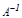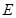матрицалары бірдей ө лшемді квадрат матрицалар.

Ескерту: Егер 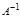матрицасы бар болса, онда ол жалғ ыз болады.

Теорема. Квадрат А матрицасына кері матрица табылуы ү шін 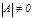болуы қ ажетті жә не жеткілікті. 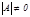болғ анда кері матрица 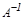былайша есептелінеді .

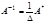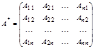Мұ ндағ ы алгебралық толық тауыштардан тү зілген матрица.

Сызық тық алгебралық тең деулер жү йесі. n белгісізі бар m тең деулер жү йесі былай жазылады:

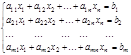
мұ ндағ ы 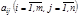жү йенің коэффициенттері, ал 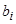- бос мү шелер деп аталады. жү йені матрицалық тү рде былай жазуғ а болады 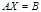немесе

, мұ ндағ ы А= жү йе матрицасы

A X B

деп аталады.

Егер сандар жиыны тең деулер жү йесін тепе-тең дікке айналдырса, онда бұ л сандар жиыны осы жү йенің шешімі деп аталады.

Егер тең деулер жү йесінің кемінде бір шешімі бар болса, онда жү йе ү йлесімді деп аталады, ал жү йенің бір де шешімі болмаса, онда жү йе ү йлесімсіз деп аталады.

Егер А матрицасын бос мү шелерден тұ ратын бағ анмен толық тырса, онда пайда болғ ан матрицаны кең ейтілген матрица дейді жә не оны 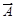деп белгілейді. Сонымен
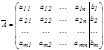