Проверка истинности параметров уравнения множественной линейной регрессии. Определение стандартных отклонений и t-статистики коэффициентов.

вторая часть вопроса) Дабы вернуть дисперсию в реальность, то есть использовать результат расчета для более приземленных целей, из нее извлекают квадратный корень. Получается так называемое стандартное отклонение. В статистике этот показатель еще называют среднеквадратическим отклонением, но первое название более короткое и распространенное. Формула стандартного отклонения имеет вид: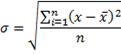

Стандартное отклонение еще называют сигмой – от греческой буквы, которой его обозначают. Отсюда и название известного статистического метода «6-сигма». То есть 6 стандартных отклонений. Стандартное отклонение, очевидно, также характеризует меру рассеяния данных, но теперь (в отличие от дисперсии) его можно сравнивать с исходными данными, так как единицы измерения у них одинаковые (это явствует из формулы расчета). Но и этот показатель в чистом виде не очень информативен, так как в нем заложено слишком много промежуточных расчетов, которые сбивают с толку (отклонение, в квадрат, сумма, среднее, корень). Тем не менее, со стандартным отклонением уже можно работать непосредственно, потому что свойства данного показателя хорошо изучены и известны. Сигма, как мера неопределенности, также участвует во многих статистических расчетах. С ее помощью устанавливают степень точности различных оценок и прогнозов. Если вариация очень большая, то стандартное отклонение тоже получится большим, следовательно, и прогноз будет неточным, что выразится, к примеру, в очень широких доверительных интервалах.

t -статистика – это отношение стандартной ошибки оценки коэффициента к его абсолютной величине. Его конкретное значение можно сравнить с таблицами t -статистик, которые в зависимости от размера выборки показывают выраженные в процентах вероятности, что оно могло возникнуть случайно, когда истинная величина коэффициента была нулевой.

Критерий Стьюдента широко применим в практике проверки статистических гипотез о равенстве средних значений двух выборок или среднего значения выборки с неким значением (целевым показателем). В последнем случае различают двухсторонние и

односторонние гипотезы. Использование данного критерия предполагает сравнение распределения наблюдаемой величины с распределением Стьюдента. В простейшем случае табличное значение критерия Стьюдента сравнивается с расчетным и, на основании этого исследователь делает вывод в пользу нулевой или альтернативной гипотезы.

Условия использования коэффициента Стьюдента:

• Исследуемые данные подчиняются нормальному закону распределения

• Равенство дисперсий (при сравнении двух выборок)

С помощью критерия Фишера оценивают качество регрессионной модели в целом и по параметрам. Для этого выполняется сравнение полученного значения F и табличного F значения. F-критерия Фишера. F фактический определяется из отношения значений факторной и остаточной дисперсий, рассчитанных на одну степень свободы: 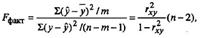, где n - число наблюдений; m - число параметров при факторе х.

F табличный - это максимальное значение критерия под влиянием случайных факторов при текущих степенях свободы и уровне значимости а.

Уровень значимости а - вероятность не принять гипотезу при условии, что она верна. Как правило а принимается равной 0, 05 или 0, 01.

Если Fтабл > Fфакт то признается статистическая незначимость модели, ненадежность уравнения регрессии.