💸 Как сделать бизнес проще, а карман толще?

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое раписание, но и напоминать клиентам о визитах тоже. Проблема в том, что средняя цена по рынку за такой сервис — 800 руб/мес или почти 15 000 руб за год. И это минимальный функционал. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
⚡️ Для новых пользователей первый месяц бесплатно. А далее 290 руб/мес, это в 3 раза дешевле аналогов. За эту цену доступен весь функционал: напоминание о визитах, чаевые, предоплаты, общение с клиентами, переносы записей и так далее.
✅ Уйма гибких настроек, которые помогут вам зарабатывать больше и забыть про чувство «что-то мне нужно было сделать».
Сомневаетесь? нажмите на текст, запустите чат-бота и убедитесь во всем сами!

Write(M);. Решение (способ 1, ручная прокрутка, перебор):

END.

Решение (способ 1, ручная прокрутка, перебор):

16) заметим, что в программе есть цикл, в котором переменная t принимает последовательно все целые значения в интервале от a до b:

for t: =a to b do begin

...

End;

17) до начала цикла в переменную M записывается значение a, а в переменную R – значение функции в точке a:

M: =a; R: =F(a);

18) внутри цикла есть условный оператор, в котором вычисляется значение функции F(t) и сравнивается со значением переменной R:

if (F(t)< R)then begin

M: =t;

R: =F(t);

End;

если новое значение функции меньше, чем значение R, в R записывается значение функции в точке t, а в переменной M запоминается само значение t (аргумент функции, соответствующий значению в R)

19) в результате анализа пп. 1-3 можно сделать вывод, что цикл ищет минимум функции F(t) на интервале от a до b, и после выполнения цикла в переменной M оказывается значение аргумента t, при котором функция достигает минимума на заданном интервале (здесь это интервал [-20, 20])

20) функция F вычисляет значение

F: =4*(x-1)*(x-3);

21) перебираем все значения t от a до b, и для каждого вычисляем соответствующее значение функции:

22) по таблице находим, что минимальное значение –4 достигается при t=2

23) таким образом, ответ: 2.

Решение (способ 2, математический анализ):

1) повторяя рассуждения пп. 1-5 из предыдущего способа решения, находим, что программа ищет значение t, при котором функция F(t) принимает минимальное значение на интервале от a до b.

2) запишем функцию в виде квадратного трёхчлена:

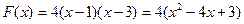
3) график этой функции – парабола, оси которой направлены вверх, поэтому функция имеет минимум

4) найдем абсциссу точки минимума, которая совпадает с абсциссой точки минимума функции

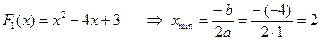
5) таким образом, ответ: 2.

Решение (способ 3, математический анализ, свойства параболы):

1) повторяя рассуждения пп. 1-5 из первого способа решения, находим, что программа ищет значение t, при котором функция F(t) принимает минимальное значение на интервале от a до b.

2) заданная функция 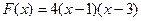имеет корни в точках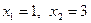

3) график этой функции – парабола, оси которой направлены вверх (коэффициент при равен 4 > 0), поэтому функция имеет минимум

4) парабола симметрична относительно вертикальной прямой, проходящей через вершину, поэтому абсцисса вершины – это среднее арифметическое корней:

5) таким образом, ответ: 2.

Ещё пример задания:

Определите, какое число будет напечатано в результате выполнения следующего алгоритма:

Var a, b, t, M, R: integer;

Function F(x: integer): integer;

Begin

F: =x*x + 4*x + 8;

End;

BEGIN

a: =-10; b: =10;

M: =a; R: =F(a);

for t: =a to b do begin

if (F(t)> R)then begin

M: =t;

R: =F(t);

End;

End;