Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
⚡️ Для новых пользователей первый месяц бесплатно. А далее 290 руб/мес, это в 3 раза дешевле аналогов. За эту цену доступен весь функционал: напоминание о визитах, чаевые, предоплаты, общение с клиентами, переносы записей и так далее.
✅ Уйма гибких настроек, которые помогут вам зарабатывать больше и забыть про чувство «что-то мне нужно было сделать».
Сомневаетесь? нажмите на текст, запустите чат-бота и убедитесь во всем сами!
Readln(K);. while (i>0) and (F(i) > K) do
|
|
while (i> 0) and (F(i) > K) do
i: =i-1;
Writeln(i);
End.
Решение:
1) заметим, что рекурсивная функция F(x) вычисляет факториал переданного ей числаx, то есть произведение x! =1× 2× 3×...× (x-1) × x
2) повторяя рассуждения предыдущей задачи, определяем, что функция выведет количество натуральных чисел, факториалы которых меньше или равны K
3) выпишем факториалы первых натуральных чисел:
1! = 1, 2! = 2, 3! = 6, 4! = 24, 5! = 120, 6! = 720, …
4) из этого ряда факториалы первых четырех чисел меньше или равны 24, поэтому при K=24 функция выведет число 4
5) программа выведет именно 4 при всех K, при которых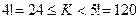 
, то есть при 
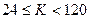; в этот диапазон входит 120-24 = 96 чисел
6) Ответ: 96.
Ещё пример задания:
Определите, какое число будет напечатано в результате выполнения следующего алгоритма:
var a, b, t, N, P: integer;
Function F(x: integer): integer;
Begin
F: = 16*(9-x)*(9-x)+127;
End;
BEGIN
a: = -25; b: = 25;
P: = 130;
N: = 0;
for t: = a to b do begin
if (F(t) > P) then begin
N: = N+1;
End;
End;
Write(N);
END.
Решение:
1) заметим, что в конце работы программы на экран выводится значение переменной N
2) в программе значение N сначала обнуляется, а затем на каждом шаге цикла увеличивается на 1 при условии, что значение функции F(t) больше значения P = 130; таким образом, N – это счётчик точек с целочисленными значениями на отрезке [-25; 25], в которых значение функции больше, чем 130
3) график функция 16*(9-x)*(9-x)+127 – парабола с ветвями вверх, минимальное значение в точке x = 9 равно 127
4) значение функции при x = 8 и x = 10 (рядом с точкой минимума) равны 16+127 = 143, поэтому только в одной точке x = 9 не выполняется условие F(t) > P
5) всего на интервале [-25; 25] есть 51 точка с целочисленными координатами; во всех, за исключением одной условие F(t) > P выполняется, то есть счётчик увеличивается на 1
6) Ответ: 50.
Ещё пример задания:
Определите, какое число будет напечатано в результате выполнения следующего алгоритма:
Var a, b, t, M, R: integer;
Function F(x: integer): integer;
Begin
F: =(x*x-4)*(x*x-4)+6;
End;
BEGIN
a: =-10; b: =10;
M: =a; R: =F(a);
for t: =a to b do begin
if (F(t)< R)then begin
M: =t;
R: =F(t);
End;
End;
write(M+6);
END.
Решение:
1) заметим, что в программе есть цикл, в котором переменная t принимает последовательно все целые значения в интервале от a до b:
for t: =a to b do begin
...
End;
2) до начала цикла в переменную M записывается значение a, а в переменную R – значение функции в точке a:
M: =a; R: =F(a);
3) внутри цикла есть условный оператор, в котором вычисляется значение функции F(t) и сравнивается со значением переменной R:
if (F(t)< R)then begin
M: =t;
R: =F(t);
End;
если новое значение функции меньше, чем значение R, в R записывается значение функции в точке t, а в переменной M запоминается само значение t (аргумент функции, соответствующий значению в R)
4) в результате анализа пп. 1-3 можно сделать вывод, что цикл ищет минимум функции F(t) на интервале от a до b, и после выполнения цикла в переменной M оказывается значение аргумента t, при котором функция достигает минимума на заданном интервале (здесь это интервал [-10, 10])
5) функция, которая используется в программе, – это квадратичная парабола: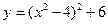 
, её ветви направлены вверх (коэффициент при 
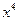положительный, равен 1); она имеет два минимума в точках 
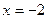и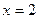 
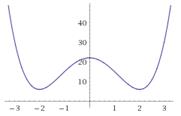
6) обе точки минимума находятся на отрезке [-10; 10], поэтому программа найдёт одну из этих точек; вопрос: какую именно?
7) для квадратичной параболы обе точки минимума имеют одинаковую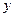 
-координату, а запоминание новой точки минимума происходит только тогда, когда только что вычисленное значение F(t) станет строго меньше, чем хранящееся в переменной R:
if (F(t) < R)then begin
M: =t;
R: =F(t);
End;
8) поэтому в точке второго минимума 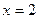никаких изменений не произойдет, и в переменной M останется значение «–2»; таким образом, будет найдет первый минимум
9) обратим внимание, что на экран выводится не M, а M+6, поэтому результат будет равен
(-2)+6=4
10) Ответ: 4.
Ещё пример задания:
Определите, какое число будет напечатано в результате выполнения следующего алгоритма:
Var a, b, t, M, R: integer;
Function F(x: integer): integer;
Begin
F: =4*(x-1)*(x-3);
End;
BEGIN
a: =-20; b: =20;
M: =a; R: =F(a);
for t: =a to b do begin
if (F(t)< R)then begin
M: =t;
R: =F(t);
End;
End;
|
|