💸 Как сделать бизнес проще, а карман толще?

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое раписание, но и напоминать клиентам о визитах тоже. Проблема в том, что средняя цена по рынку за такой сервис — 800 руб/мес или почти 15 000 руб за год. И это минимальный функционал. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
⚡️ Для новых пользователей первый месяц бесплатно. А далее 290 руб/мес, это в 3 раза дешевле аналогов. За эту цену доступен весь функционал: напоминание о визитах, чаевые, предоплаты, общение с клиентами, переносы записей и так далее.
✅ Уйма гибких настроек, которые помогут вам зарабатывать больше и забыть про чувство «что-то мне нужно было сделать».
Сомневаетесь? нажмите на текст, запустите чат-бота и убедитесь во всем сами!

Readln(x);. if M < (x mod 10) then begin

L: =0; M: =0;

while x > 0 do begin

L: =L+1;

if M < (x mod 10) then begin

M: =x mod 10;

End;

x: = x div 10;

End;

Writeln(L); write(M);

End.

Решение:

1) для решения задачи необходимо понять, что делает эта программа

2) если это не видно сразу, можно выполнить ручную прокрутку для какого-то простого числа, например, для числа 251:

3) можно догадаться, что в результате работы программы в переменной L окажется число цифр числа, а в переменной M – наибольшая цифра, но это предположение нужно постараться доказать

4) нужно вспомнить (и запомнить), что для целого числа 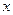остаток от деления на 10 (x mod 10) – это последняя цифра в десятичной записи числа, а целочисленное деление (x div 10) отсекает последнюю цифру, то есть из 123 получается 12

5) рассмотрим цикл, число шагов которого зависит от изменения переменной x:

while x > 0 do begin

...

x: = x div 10; { отсечение последней цифры }

End;

здесь оставлены только те операторы, которые влияют на значение x

6) из приведенного цикла видно, что на каждом шаге от десятичной записи x отсекается последняя цифра до тех пор, пока все цифры не будут отсечены, то есть x не станет равно 0; поэтому цикл выполняется столько раз, сколько цифр в десятичной записи введенного числа

7) на каждом шаге цикла переменная L увеличивается на 1:

L: =L+1;

других операторов, меняющих значение L, в программе нет; поэтому после завершения цикла в переменной L действительно находится количество цифр

8) теперь разберемся с переменной M, которая сначала равна 0; оператор, в котором она меняется, выглядит так:

if M < (x mod 10) then begin

M: =x mod 10;

End;

учитывая, что x mod 10 – это последняя цифра десятичной записи числа, получается что если эта цифра больше, чем значение M, она записывается в переменную M;

9) этот оператор выполняется в цикле, причем выражение x mod 10 по очереди принимает значения всех цифр исходного числа; поэтому после завершения циклам в переменной M окажется наибольшая из всех цифр, то есть наша догадка подтверждается

10) итак, по условию задачи фактически требуется найти наибольшее трехзначное число, в котором наибольшая цифра – 7; очевидно, что это 777.

11) ответ: 777.

Ещё пример задания:

P-00. Ниже записана программа. Получив на вход число 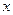, эта программа печатает два числа, 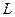и 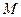. Укажите наибольшее из таких чисел 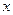, при вводе которых алгоритм печатает сначала 3, а потом 120.

var x, L, M: integer;

Begin